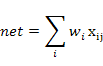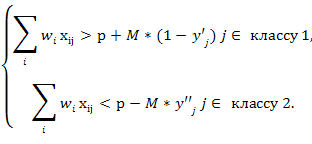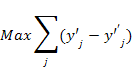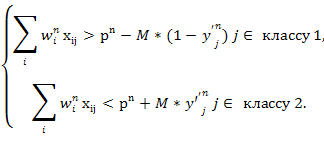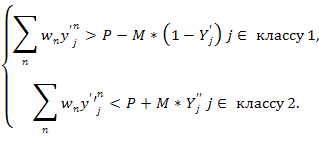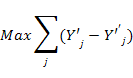Применение нейронных сетей к задачам оценки вероятности дефолта по потребительским кредитам
Чернавин Федор Павлович,
аспирант Уральского федерального университета им. первого Президента России Б. Н. Ельцина, г. Екатеринбург.
Введение
В 2011-2012 годах в России наблюдался стремительный рост объемов розничных кредитных портфелей. Так, за период с 01.01.2011 по 01.01.2013 объемы судной задолженности по кредитам физических лиц увеличились в 2 раза с 3 725 млрд. руб. до 7 493 млрд. руб. Заметим, что к концу 2012 года темпы прироста объемов ссудной задолженности замедлись, а за январь 2013 увеличились только на 0,9% (с 7 493 млрд. руб. до 7 557 млрд. руб.)
На фоне значительных темпов прироста розничных кредитных портфелей увеличивались и объемы просроченной задолженности (с 285 млрд. руб. на 01.01.2011 до 334 млрд. руб. на 01.01.2013). При этом доля просроченной задолженности, начиная с 2013 года, имеет тенденцию к увеличению, так на 01.01.2013 доля просроченной задолженности составляла 4,6%, тогда как на 01.04.2013 доля просроченной задолженности увеличилась до 4,9%.
Рост неплатежей по кредитам ставит перед банками задачу улучшения качества оценки кредитного риска заемщиков на этапе выдачи кредита.
Для оценки вероятности дефолта (перехода на срок свыше 180 дней) в течение года с момента выдачи кредита нами по кредитным договорам за 2011 год была обучена двухслойная нейронная сеть, состоящая из нейронов с пороговой функцией активации. Размер обучающей выборки составил около 1 500 кредитных договоров, размер тестовой выборки составил свыше 150 000 кредитных договоров, при этом количество дефолтов составляло около 0,8% на выборках.
1. Теоретические основы нейронных сетей
1.1. Формальный нейрон Маккалока и Питтса
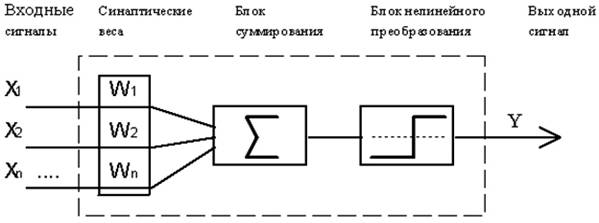
Рис. 1.
В блоке суммирования происходит накопление общего входного сигнала (обычно обозначаемого символом net), равного взвешенной сумме входов:
|
|
(1) |
Геометрическая интерпретация формального нейрона – гиперплоскость. Отклик нейрона далее описывается по принципу «все или ничего», т. е. переменная подвергается нелинейному пороговому преобразованию, при котором выход (состояние активации нейрона) Y устанавливается равным единице, если net > p, и Y=0 в обратном случае.
|
|
(2) |
Математическая запись формального нейрона с пороговой функцией активации выглядит следующим образом:
|
|
(3) |
где M – некоторое очень большое число, y’,y” – булевы переменные (значения активационной функции). Очевидно, что необходимо стремится к минимизации ошибки классификации, то есть нахождению таких весов w, чтобы точки одного класса находились выше гиперплоскости, а точки второго класса ниже гиперплоскости:
|
|
(4) |
Геометрическая интерпретация для линейно неразделимых множеств показана на рис. 2.
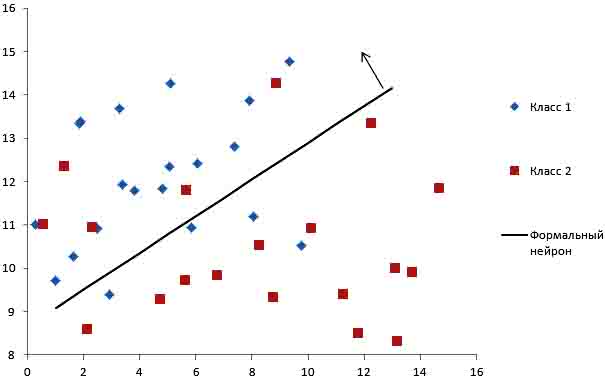
Рис. 2. Классификация формальным нейроном линейно неразделимых множеств. Стрелочкой на рисунке указывается «верх» гиперплоскости, то есть область, в которых y принимает значение 1.
Для решения задачи нахождения максимума качества классификации можно применить методы целочисленного математического программирования, такие как метод ветвей и границ и метод Гомори.
1.2. Архитектура искусственной нейронной сети
Искусственная нейронная сеть представляет собой систему соединённых и взаимодействующих между собой формальных нейронов. Каждый нейрон подобной сети имеет дело только с сигналами, которые он периодически получает, и сигналами, которые он периодически посылает другим процессорам. И, тем не менее, будучи соединёнными в достаточно большую сеть с управляемым взаимодействием, такие локально простые нейроны вместе способны выполнять довольно сложные задачи.
Для решения задачи оценки вероятности дефолта в течение года с момента выдачи кредита нами используется искусственная нейронная сеть со следующей архитектурой (рис. 3).
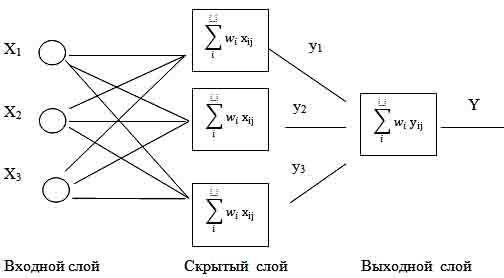
Рис. 3. Архитектура нейронной сети. Для нашей задачи: X – входные параметры заемщика, y1..3 – решения нейронов, Y4 – решение нейронной сети.
1.3. Обучение искусственной нейронной сети
Часто для обучения нейронной сети используется метод обратного распространения ошибки. Данный метод обучения чаще всего применяется непрерывных активационных функций Y, поскольку для модификации весов w необходимо вычислять разницу между идеальным и полученным значениями выхода нейронной сети.
Задачу обучения данной нейронной сети с пороговой функцией активации можно свести к задаче линейного частично-целочисленного программирования следующего вида.
|
|
|
|
|
|
|
|
(5) |
где n – номер нейрона скрытого слоя, P – «порог» для выходного слоя сети, Y – булева переменная (значение активационной функции выходного слоя).
![]() вида
вида ![]() является нелинейной, поэтому для решения задачи
частично-целочисленного программирования она не применима. Поскольку
является нелинейной, поэтому для решения задачи
частично-целочисленного программирования она не применима. Поскольку ![]() являются булевыми переменными, то можно, выполнив соответствующие
преобразования, расписать
являются булевыми переменными, то можно, выполнив соответствующие
преобразования, расписать ![]() в виде двух переменных и решать задачу линейного
частично-целочисленного программирования, но для упрощения задачи обучения
нейронной сети все веса выходного слоя устанавливаются равными 1
в виде двух переменных и решать задачу линейного
частично-целочисленного программирования, но для упрощения задачи обучения
нейронной сети все веса выходного слоя устанавливаются равными 1
Далее приведем геометрические интерпретации решений данной нейронной сети на плоскости.
На рисунке 4 построена нейронная сеть из 5 нейронов. N1..N5 – нейроны (гиперплоскости). Пороговая переменная сети P приняла значение 2. На рисунке 5 построена нейронная сеть из 5 нейронов. Пороговая переменная сети P приняла значение 3.
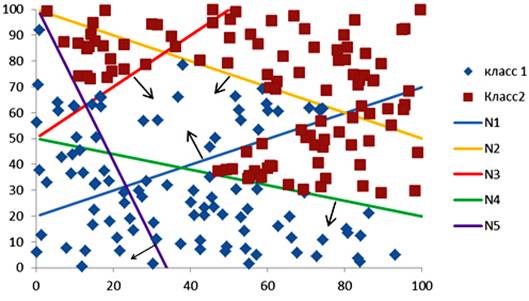
![]() Рис. 4. Классификация нейронной сетью на плоскости.
Рис. 4. Классификация нейронной сетью на плоскости.
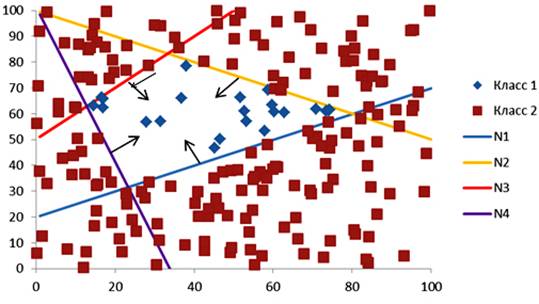
Рис. 5. Классификация нейронной сетью на плоскости.
2.1. Имеющиеся данные
У нас имеются данные по 152 560 кредитным договорам по потребительским кредитам без обеспечения, выданным в период с 01.01.2011 по 01.01.2012, по которым было допущено 1240 случаев дефолта (0,8%). При этом у нас имеется информация только о сумме кредита, сроке кредита, возрасте заемщика и территории, на которой выдан кредит. Кредиты были выданы на территориях Свердловской области, Челябинской области, Курганской области, и Республики Башкортостан, при этом отдельно выделяются кредиты, выданные в крупных городах (Екатеринбург, Уфа, Челябинск).
Для учета различных экономических условий на территориях и времени, нами в качестве параметра рассматривается не сама сумма кредита, а ее размер относительно средней суммы кредита выданной на территории в предыдущем месяце.
Под дефолтами нами понимаются случаи выхода кредитного договора на сроки свыше 180 дней в течение 12 месяцев с момента выдачи кредитного договора.
Заметим, что хотя обычно под дефолтом понимается неисполнение заемщиком обязательств по кредитному договору свыше 90 дней, что определено пунктом 452 Базеля 2, но в соответствии с Базелем 2 в случае с розничными обязательствами органы надзора могут применять срок до 180 дней для различных продуктов в зависимости от местных условий. По нашему мнению в российских условиях корректнее использовать срок свыше 180 дней, поскольку, исходя из практики, более 50% заемщиков допустивших случаи выхода на просрочку свыше 90 дней погасят просроченную задолженность, не переходя на сроки свыше 180 дней. Это связано с низкой платежной дисциплиной заемщиков в Российской Федерации.
2.2. Результаты оценки вероятности дефолта
Для построения комитета большинства нами был взят 3% от всей имеющейся выборки, что составило 26 кредитов со случаями дефолта и 4500 кредитов без случаев дефолта.
Нами были обучены нейронные сети из 3 и 5 нейронов.
На тестовой выборке из 140 000 кредитных договоров для нейронной сети из 3 нейронов доля решений нейронной сети за отсутствие дефолта составила 80,2%, при этом число дефолтов в данной группе составила 0,6%. Доля решений нейронной сети за возникновение дефолта составила 19,8%, при этом число дефолтов в данной группе составило 1,8%.
На тестовой выборке из 140 000 кредитных договоров для нейронной сети из 5 нейронов доля решений нейронной сети за отсутствие дефолта составила 66,5%, при этом число дефолтов в данной группе составила 0,5%. Доля решений нейронной сети за возникновение дефолта составила 33,5%, при этом число дефолтов в данной группе составило 1,4%.
В целом с увеличением числа нейронов в сети возможно лучше обозначить группу, в которой вероятность дефолта ниже средней. Заметим, что полученные результаты далеки от практического применения, что во многом связано с малым количеством параметров заемщика. С увеличением числа параметров можно ожидать возрастание точности нейронной сети.
Заключение
Нами было рассмотрено применение нейронных сетей для оценки вероятности дефолта по заемщикам физическим лицам. Нейронные сети были обучены методом удобным для реализации в пакетах математического программирования.
В целом применение нейронных сетей представляет практический интерес для банков, поскольку улучшение качества классификации заемщиков позволит уменьшить долю неплатежей и, следовательно, увеличить прибыль банка.
Хотелось бы отметить, что нами для прогнозирования использовались только 3 параметра заемщиков – сумма кредита, возраст заемщика и срок кредита. При этом обучающая выборка составила только 3% от общего числа кредитов. С введением дополнительных переменных, описывающих заемщика, таких как доходы, кредитная история, пол, образование и т.д. ожидается увеличение качества решения.
Литература
1. Хайкин Саймон. Нейронные сети. Полный курс - М.: ООО «И. Д. Вильямс» 2006.
2. Чернавин Ф.П. Применение метода комитета большинства для принятия решения по выдаче кредита / Доклады всероссийской научной конференции АИСТ’12. Екатеринбург, 4-6 апреля 2013 года. С.93-96.
3. Ablow CM. and Kaylor D.J., Inconsistent Homogenous Linear Inequalities / Bulletin of the American Mathematical Society, 1965, vol. 71, no 5, p. 724.
4. Warren S. McCulloch, Walter Pitts, A logical calculus of the ideas immanent in nervous activity / The bulletin of mathematical biophysics, 1943, vol. 5, Issue 4, p 115.
Поступила в редакцию 11.07.2013 г.