Математическая модель расчета динамики двухпозиционных электромагнитных актуаторов вакуумных выключателей среднего напряжения
Байда Евгений Иванович,
кандидат технических наук, доцент кафедры «Электрические аппараты» Харьковского национального технического университета «НТУ ХПИ».
В настоящее время значительный сегмент рынка выключателей среднего напряжения составляют вакуумные автоматические выключатели [Назарычев А. Н.]. По конструкции привода такие выключатели можно классифицировать: выключатели с пружинно-моторным актуатором и механической защелкой; выключатели с электромагнитным актуатором и механической защелкой; выключатели с поляризованным бистабильным актуатором, у которого роль механической защелки выполняет высококоэрцитивный постоянный магнит.
Последний тип актуаторов широко используется фирмой АББ [Вакуумный выключатель VM1] и имеет ряд существенных преимуществ (простота и надежность конструкции) по сравнению с другими типами (рис.1).
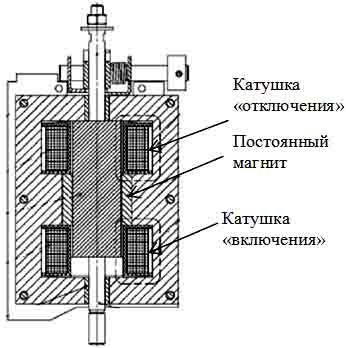
Рис. 1. Поляризованный двухпозиционный актуатор.
Такой актуатор запатентован фирмой АББ и сложен в производстве. В этой связи были предложены альтернативные конструкции актуаторов [Бугайчук В.Н., Клименко Б.В.], показанные на рис. 2 в цилиндрической системе координат.
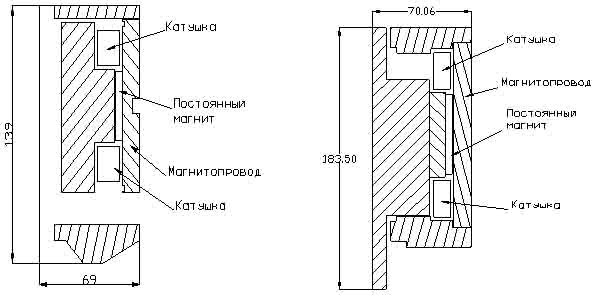
а) б)
Рис. 2. Двухпозиционные бистабильные поляризованные актуаторы: а) асимметричный актуатор с внешним якорем; б) симметричный актуатор с внутренним якорем.
Удержание якоря в конечных положениях осуществляется за счет энергии постоянных магнитов, а напряжение на катушки подается на короткое время для изменения положения якоря.
При проектировании такого рода устройств недостаточно проведение только статических расчетов. Основными являются динамические расчеты, позволяющие детально разобраться в физике происходящих процессов и сделать окончательный вывод о работоспособности конструкции. Расчеты такого рода могут быть проведены только на основании соответствующих математических моделей, в основе которых лежат уравнения электромагнитного поля, уравнения электрической цепи и уравнения движения [Байда Е.И.]. Сложность заключается в необходимости проведения расчетов электромагнитного поля в неоднородной, нелинейной, проводящей или непроводящей среде с учетом движения расчетных областей и наличия постоянных магнитов.
Целью данной статьи является описание математической модели расчета динамики поляризованного бистабильного актуатора, построенного на базе высококоэрцитивных постоянных магнитов.
Расчетные уравнения низкочастотного электромагнитного поля.
1. Неподвижная часть магнитопровода:
, (1)
где s – проводимость; 
– векторный магнитный
потенциал; mr=mr(||B||) – относительная
магнитная проницаемость.
2. Движущаяся часть магнитопровода (якорь):
. (2)
Преобразуем полученное выражение с помощью соотношений векторной алгебры [Френкель Я.И.]:
,
но
,
где 
– скорость движения
якоря.
Так как скорость движения якоря зависит только от времени и не зависит от координат, то:
,
но
,
поэтому
.
Следовательно, в окончательном варианте расчетное уравнение запишется:
. (3)
3. Катушки электромагнита можно считать «плохим» немагнитным проводником с плотностью тока, определяемого сторонними источниками:
, (4)
где i – ток катушки; w – число витков катушки; S – сечение катушки.
4. Область постоянного магнита можно представить как проводящую неподвижную среду, имеющую априори заданную намагниченность, тогда:
,
где 
– остаточная
магнитная индукция.
В этом случае:
. (5)
5. Уравнение для среды, окружающей магнит:
. (6)
В расчетах электромагнитных систем достаточно часто значение поля не является целью расчета. Как правило, необходимо определить значение электромагнитных сил, действующих на одну из частей системы. Для этого необходимо воспользоваться наиболее универсальной формулой – тензором натяжения Максвелла:
, (7)
где 
– значение
электромагнитной силы; 
– вектор внешней нормали к поверхности
интегрирования 
.
Система уравнений (1-7) должна быть дополнена начальным и граничными условиями (условие аксиальной симметрии и значением поля на границе расчетной области).
Расчетные уравнения электрической цепи.
В уравнении (4) присутствует плотность тока сторонних источников, которая определяется уравнением электрической цепи. Уравнение электрической цепи для катушки электромагнита:
, (8)
где U – напряжение источника; e – противоэдс, наводимая в катушке; Re – активное сопротивление внешней цепи; Rk – активное сопротивление катушки; i – ток катушки; Le – индуктивность внешней цепи.
Необходимо отметить, что источником напряжения может быть постоянное напряжение, выпрямленное переменное напряжение либо предварительно заряженный конденсатор. Поэтому:
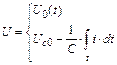, (9)
где U0 (t) – постоянное, либо выпрямленное напряжение; Uс0 – начальное напряжение на конденсаторе; С – емкость конденсатора.
Что касается значения противоэдс, то в соответствии с законом Фарадея:
, (10)
где w – число витков катушки; FY – поток, приведенный по потокосцеплению, т.е. поток, связанный со всеми витками катушки.
Определим этот поток следующим образом:
, (11)
где F – магнитный поток, охваченный витками катушки; S – площадь поперечного сечения катушки.
Согласно теореме Стокса, связь между потоком векторного поля через ориентированную поверхность и циркуляцией этого поля по краю поверхности, можно представить в виде:
, (12)
где 
– площадь,
пронизываемая магнитным потоком; 
– направление обхода контура циркуляции
вектора .
Следовательно, формулу (10) с учетом (11-12) можно представить:
, (13)
где 
– проекция векторного
магнитного потенциала на направление обхода контура; V – объем катушки.
Окончательно расчетное уравнение для электрической цепи запишется в виде с учетом (9):
. (14)
Начальные условия для уравнения (14) нулевые.
Уравнения механической цепи.
Конструкция привода вакуумного выключателя представляет собой многозвенный механизм, при расчетах которого необходимо учитывать инерционность всех движущихся частей. Основным является уравнение движения якоря электромагнита:
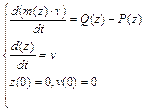, (15)
где 
– перемещение якоря; 
– скорость якоря; 
– масса движущихся
частей, приведенная к якорю; – скорость якоря; 
– электромагнитная сила; 
– противодействующая
сила, приведенная к якорю.
Уравнение (15) представляет собой уравнение одномерного движения с переменной массой. Для удобства расчетов оно может быть переписано в виде:
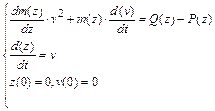. (16)
Полученные уравнения (1-16) представляют собой систему уравнений и являются математической моделью динамики рассматриваемых актуаторов (рис. 2). На основании уравнений (1-16) может быть получено решение широкого круга задач, таких как расчеты индукционно – динамических систем, магнитно импульсной обработки материалов и т.п.
Получить решение уравнений (1-16) достаточно сложно, так как возникают проблемы с точностью, сходимостью и устойчивостью системы.
Решения системы (1-16) было получено с использованием метода конечных элементов для интегрирования по пространственным переменным и усовершенствованного метода Гира, называемого BDF (Backward Differentiation Formula) [Ракитский Ю.В.] по времени. При интегрировании системы необходимо избегать скачкообразного изменения параметров (например, изменение приведенной массы при замыкании главных контактов). В этом случае необходима аппроксимация перехода непрерывной гладкой (вплоть до второй производной) функцией (рис. 3), при использовании которой скачок функции «размывается» на определенном пространственном либо временном интервале.
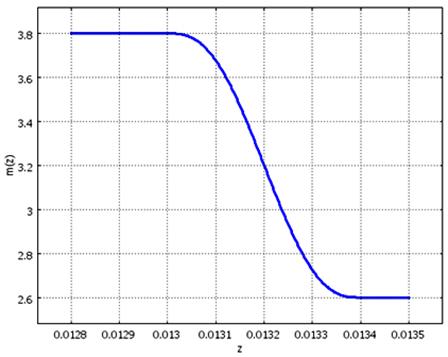
Рис. 3. Пример аппроксимации изменения массы.
Изначально метод конечных элементов был плохо адаптирован для решения нестационарных задач [Митчелл Э., Сегерлинд Л., Сильвестр П.]. Решением данной проблемы является использование «деформируемой» сетки. Суть метода заключается в том, что подвижные области представляются расположенными в некотором эластичном пространстве, покрытом сеткой. При изменении положения области, сетка, принадлежащая области остается неизменной, а координаты сетки, принадлежащие границам подвижных областей, претерпевают деформацию в соответствии с заданным законом движения, определяемого уравнением (16) (рис. 4).
а) б)
Рис. 4. Деформация сетки: а) исходная сетка; б) деформированная сетка.
Из теории метода конечных элементов известно [Митчелл Э., Сегерлинд Л., Сильвестр П.], что размер и форма ячеек сетки существенно влияют на точность расчетов, поэтому при движении области на каждом временном шаге необходимо проверять «качество» сетки, перестраивая сетку по мере необходимости.
На основании изложенного материала были проведены расчеты динамики актуаторов, некоторые результаты которых показаны на рис. 5.
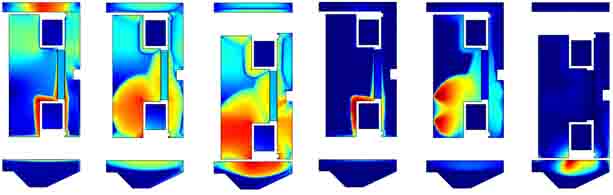
Рис. 5. Расчет магнитной индукции и вихревых токов при включении актуатора: а) модуль магнитной индукции в моменты времени 2 мс, 20 мс, 33 мс.; б) вихревой ток магнитопровода в моменты времени 2 мс, 20 мс, 33 мс.
Выводы
По разработанной математической модели были проведены расчеты динамики бистабильных актуаторов на базе высококоэрцитивных постоянных магнитов, позволившие создать работоспособные конструкции актуаторов в соответствии с требованиями технического задания.
Литература
1. Байда Е.И. Расчет переходных процессов в электромагнитном механизме на основании уравнений электромагнитного поля / Е.И. Байда Электротехника и электромеханика. – Харків: НТУ «ХПІ», 20008. - №6. С.-39-43.
2. Байда Е.И. Влияние проводимости материала на динамические характеристики электромагнитных механизмов постоянного тока / Е.И. Байда Электротехника и электромеханика. – Харків: НТУ «ХПІ», 2010. - №1. С.-3-5.
3. Байда Е.И. Моделирование динамических характеристик электромагнитных механизмов постоянного тока с магнитной защёлкой / Е.И. Байда Электротехника и электромеханика. – Харків: НТУ «ХПІ», 2010. - №2. С.-3-5.
4. Байда Е.И. Моделирование процесса отключения электромагнита постоянного тока с магнитной защёлкой / Е.И. Байда Электротехника и электромеханика. – Харків: НТУ «ХПІ», 2010. - №3. С.-6-9.
5. Байда Е.И. Расчет динамики двухпозиционного электромагнита постоянного тока с магнитной защёлкой / Е.И. Байда Электротехника и электромеханика. – Харків: НТУ «ХПІ», 2010. - №4. С.-10-12.
6. Байда Е.И. Влияние формы напряжения источника питания на динамические характеристики электромагнита постоянного тока / Е.И. Байда Электротехника и электромеханика. – Харків: НТУ «ХПІ», 2010. - №5. С.-3-4.
7. Байда Е.И. Математические модели подключения источников бистабильных поляризованных актуаторов к источникам энергииэнергии / Е.И. Байда Вісник Національного технічного університету «Харківський політехнічний інститут». – Харків: НТУ «ХПІ», 2012. - №49.
8. Бугайчук В.Н. Обоснование целесообразности использования обмоток включения и отключения бистабильных электромагнитных приводах вакуумных выключателей / Бугайчук В.Н. , Клименко Б.В., Емельянов В.Л. Електротехніка і електромеханіка – 2011. – №3. – С. 21 – 24.
9. Вакуумный выключатель VM1 с электромагнитным приводом [Электронный ресурс] – Режим доступа: http://www05.abb.com/.
10. Клименко Б.В. Электромагнитные приводы вакуумных выключателей средних напряжений / Б.В. Клименко, В.М. Бугайчук, А.М. Гречко Вестник НТУ «ХПИ». – 2004. – № 42. – С. 73 – 80.
11. Клименко Б.В. Опытный образец двухпозиционного электромагнитного привода вакуумного выключателя среднего напряжения / Клименко Б.В., Гречко А.М., Бугайчук В.М. Електротехніка і електромеханіка – 2005. – №2. – С. 23 – 28.
12. Клименко Б.В. Быстродействующий электромагнитный привод с вытеснением магнитного поля для вакуумного выключателя среднего напряжения/ Клименко Б.В., Гречко А.М., Бугайчук В.М., Выровец С.В. Електротехніка і електромеханіка – 2006. – №4. – С. 22 – 26.
13. Клименко Б.В. Электромагнитный привод с двухпозиционной магнитной защелкой для вакуумного выключателя среднего напряжения/ Клименко Б.В., Гречко А.М., Ересько А.В. Електротехніка і електромеханіка – 2007. – №6. – С. 40 – 43.
14. Митчелл Э. Метод конечных элементов для уравнений с частными производными / Э. Митчелл, Р. Уэйт. – М.: Мир, 1981. – 216 с.
15. Назарычев А. Н. Анализ основных преимуществ вакуумных выключателей. [Электронный ресурс] / Назарычев А. Н. БЭСТЕР Комплект. – Режим доступа к журн.: http://www.bester54.ru/cms.php?type=page&id=22.
16. Ракитский Ю.В. Численные методы решения жестких систем/ Ракитский Ю.В., Устинов C.M., Черноруцкий И.Г. - M.: Hаука, 1979.
17. Сегерлинд Л. Применение метода конечных элементов / Сегерлинд Л. – М.: Мир, 1979. – 392 с.
18. Сильвестр П. Метод конечных элементов для радиоинженеров и инженеров электриков / П. Сильвестр, Р. Феррари. – М.: Мир, 1986. – 229 с.
19. Френкель Я.И. Курс теоретической механіки / Френкель Я.И. – Ленинград: Типография «Красный печатник», 1939. – 386 с.
Поступила в редакцию 14.01.2013 г.