Моделирование процесса отключения моностабильного электромагнитного актуатора с постоянными магнитами

Моделирование процесса отключения моностабильного электромагнитного актуатора с постоянными магнитами

Байда Евгений Иванович,

кандидат технических наук, доцент кафедры Электрические аппараты Харьковского национального технического университета «НТУ ХПИ»,

Украина.

В статье рассматривается вопрос математического моделирования процесса отключения моностабильного электромагнитного актуатора с постоянными магнитами путем разряда на его катушку ёмкостного накопителя энергии. Приведены динамические характеристики процесса отключения. Даны количественные и качественные оценки полученных результатов.

В настоящее время одним из наиболее перспективных видов актуаторов являются поляризованные актуаторы на базе высококоэрцитивных постоянных магнитов [Пищур А.П., АББ Ревю, Клименко Б.В.]. Такие актуаторы характеризуются значительными электромагнитными силами в стабильных состояниях; минимальными затратами энергии (стабильные состояния обеспечиваются постоянными магнитами); высокой надежностью за счет малого количества механических деталей и простотой конструкции. К недостаткам данных актуаторов можно отнести сложность их проектирования по заданным характеристикам. Это связано с необходимостью проведения динамических расчетов магнитных, электрических и механических параметров в неоднородных, нелинейных, проводящих движущихся средах с учетом постоянных магнитов. Такой анализ возможен только на базе мультифизических моделей решения системы уравнений электромагнитного поля, электрической цепи и механики движения тела с переменной массой [Байда Е.И.]. Ввиду того, что удержание якоря осуществляется за счет энергии постоянного магнита, отключение таких систем осуществляется, как правило, путем разряда на катушку ёмкостного накопителя энергии соответствующей полярности. Для успешного отключения такого электромагнита необходимо правильно выбрать ёмкость и напряжение конденсатора с учетом электрических и магнитных параметров катушки и динамических характеристик движущихся элементов.

Решение данной задачи актуально, так как позволяет понять физику процессов, происходящих в актуаторе, а так же определить оптимальные параметры системы, существенно сэкономив на экспериментальных образцах.

Научная новизна заключается в комплексном подходе к решению поставленной задачи.

Постановка задачи – провести расчет динамики отключения моностабильного поляризованного актуатора, катушка которого включается на ёмкостной накопитель энергии с учетом проводимости и нелинейных свойств материала магнитопровода. Цель – получить динамические характеристики отключения спроектированного актуатора. Внешний вид половины актуатора показан на рис. 1. Корпус и сердечник магнита крепятся на немагнитном основании. Наличие воздушного шунта обусловлено встречными направлениями потоков постоянного магнита и катушки в режиме отключения и гарантирует стабильность характеристик постоянного магнита.

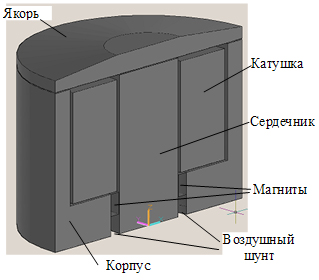
Рис. 1. Моностабильный актуатор.

Расчетные уравнения.

1. Неподвижная часть магнитопровода:

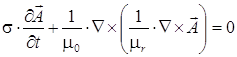, (1)

где s – проводимость; – векторный магнитный потенциал; m_r=m_r(||B||) – относительная магнитная проницаемость и является нелинейной функцией, зависящей от магнитной индукции.

2. Движущаяся часть магнитопровода (якорь):

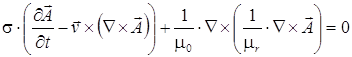, (2)

где – скорость движения якоря актуатора, определяемая на основании решения уравнений движения.

3. Катушку электромагнита можно считать «плохим» немагнитным проводником с равномерно распределенной по сечению плотностью тока, определяемого сторонними источниками:

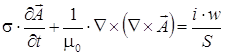, (3)

где i – ток катушки; w – число витков катушки; S – сечение катушки.

Проводимость, для устранения сингулярности расчетной матрицы, должна быть малой, но не нулевой величиной.

4. Область постоянного магнита можно представить как проводящую неподвижную среду с априори заданной намагниченностю:

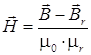, (4)

где – остаточная магнитная индукция.

В этом случае:

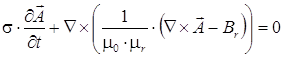(5)

5. Уравнение для окружающей среды:

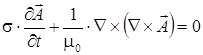. (6)

Проводимость, для устранения сингулярности матрицы, должна быть малой, но не нулевой величиной.

В расчетах электромагнитных систем значение поля не являются целью расчета. Как правило, необходимо определить значение электромагнитных сил, действующих на одну из частей системы. Для этого необходимо воспользоваться наиболее универсальной формулой – тензором натяжения Максвелла:

(7)

где – значение электромагнитной силы; – вектор внешней нормали к поверхности интегрирования .

6. Уравнение электрической цепи:

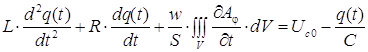, (8)

где q(t) – количество электричества; R – активное сопротивление катушки и внешней цепи;L – индуктивность внешней цепи; w – число витков катушки; S – площадь поперечного сечения катушки; V – объем катушки; U_с₀ – начальное напряжение на емкости; С – емкость конденсатора.

7. Уравнения движения якоря:

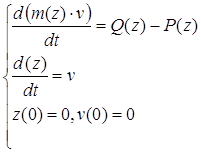, (9)

где m(z) – приведенная масса якоря; Q(z) – электромагнитная сила; P(z) – противодействующая сила; z – перемещение якоря; v – скорость якоря.

Для однозначности решения задача должна быть дополнена начальными условиями, которые для уравнений поля запишутся в виде:

, (10)

где f(r, z) – распределение магнитного потенциала в расчетных областях при обесточенной катушке и притянутом якоре, полученное на основании решения стационарной задачи и нулевых условий для уравнения динамики.

Исходные данные: приведенная масса якоря – 0,3 кг; активное сопротивление катушки – 100 Ом; число витков – 3000; напряжение на емкости – 90 В; емкость – 50×10^-6 Ф; противодействующая сила – 100 Н, ход якоря – 5мм, внешняя индуктвность – 0.01 мГн.

Для ферромагнитного сердечника и якоря задавалось значение относительной магнитной проницаемости в функции модуля магнитной индукции. Расчеты динамики проводились для электрической проводимости материала электромагнита равной 10 МS/m.

Решение задачи проводилось численными методами (метод конечных элементов) в нестационарном режиме на деформируемой сетке решателем с автоматическим (в зависимости от точности получаемого результата) выбором шага (метод BDF).

Результаты расчета в начальный момент времени показаны на рис. 2.

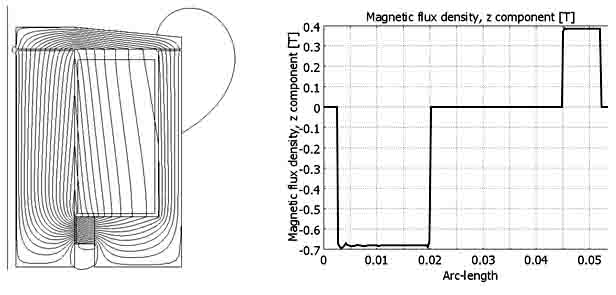
а) б)

Рис. 2. Начальное распределение поля в актуаторе а) и осевой составляющей магнитной индукции в среднем сечении б).

Из рис. 2 следует: магнитный поток равномерно распределен по площади поперечного сечения магнитопровода; практически весь поток постоянного магнита протекает через рабочие воздушные зазоры; магнитный поток, замыкающийся через шунт незначителен.

Результаты расчета динамики отключения актуатора показаны на рис. 3.

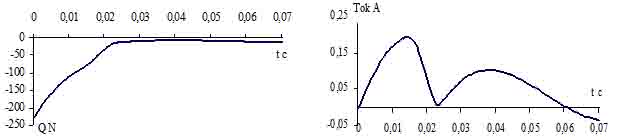
а) б)

Рис. 3. Изменение удерживающей силы а) и тока катушки б) в процессе отключения актуатора.

Как следует из рис. 3, при принятых параметрах разрядного конденсатора, электромагнитная сила изменяется от минус 220 Н до минус 7 Н, что обеспечивает надежность процесса отключения, а трогание якоря (равенство противодействующей и электромагнитной сил) начинается через 10,5 мс после начала разряда конденсатора.

На рис.4 показано изменения напряжения на конденсаторе и ход якоря в функции времени.

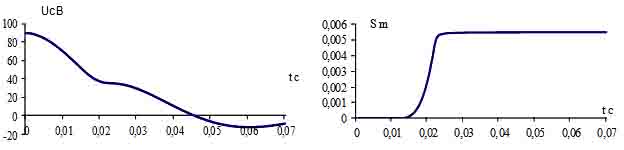
а) б)

Рис. 4. Значение напряжения на конденсаторе а) и хода якоря б) в функции времени

Из рис.4 следует, что отключение актуатора происходит за 25 мс, при этом, конденсатор может быть отсоединен от катушки, так как в дальнейшем возможен его перезаряд.

Ввиду противоположности направление потоков постоянного магнита и катушки, интерес представляют значения осевой составляющей магнитной индукции в среднем сечении магнита, показанные на рис. 5.

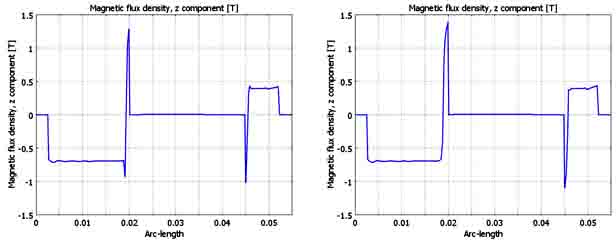
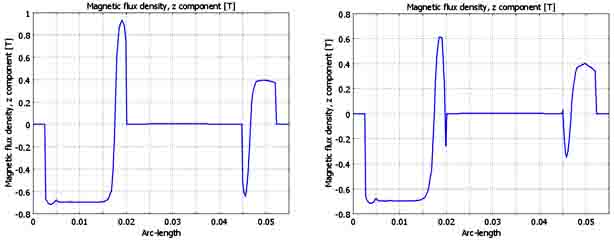
а) б)

Рис. 5. Распределение осевой составляющей магнитной индукции в моменты времени: а) – 5мс; б) – 10мс; в) – 50мс; г) – 70 мс.

Из рис. 5 следует, что и индукция распределена по сечению магнитопровода крайне неравномерно, что свидетельствует о явно выраженном магнитном поверхностном эффекте.

Выводы

На базе разработанной мультифизической модели динамики отключения моностабильного магнита были проведены расчеты по определению времени отпускания якоря, оптимизации значений ёмкости конденсатора и напряжения его заряда необходимых для срабатывания актуатора, позволившие создать опытный образец конструкции, подтвердивший, в пределах инженерной точности, результаты расчета.

Литература

1. Практическое применение вакуумных выключателей [Электронный ресурс] / А.П. Пищур // Техн. библ. комп. пром. группы Таврида Электрик 2005. – Режим доступа: http://tavrida.eu/doc/article_pishchur_ISM Application_ru.pdf.

2. Лучшие инновации 2004 года [Электронный ресурс] / АББ Ревю. – 2005. – № 1. – С. 43. Режим доступа к журн.: http://abbreview.ru/archive /2005/1/p43.pdf.

3. Клименко Б.В. Электромагнитные приводы вакуумных выключателей средних напряжений / Б.В. Клименко, В.М. Бугайчук, А.М. Гречко // Вестник НТУ «ХПИ». – 2004. – № 42. – С. 73 – 80.

4. Байда Е.И. Расчет переходных процессов в электромагнитном механизме на основании уравнений электромагнитного поля / Е.И.Байда // Электротехника и электромеханика. – Харків: НТУ «ХПІ», 20008. - №6. С.-39-43.

5. Байда Е.И. Моделирование динамических характеристик электромагнитных механизмов постоянного тока с магнитной защёлкой / Е.И.Байда // Электротехника и электромеханика. – Харків: НТУ «ХПІ», 2010. - №2. С.-3-5.

Поступила в редакцию 14.06.2013 г.