Описание синхронного генератора в обобщенных параметрах

 

Вилесов Дмитрий Васильевич,

доктор технических наук, профессор,

Бондаренко Александр Евгеньевич,

кандидат технических наук.

Санкт-Петербургский государственный морской технический университет.

 

Под обобщенными параметрами трехфазного синхронного генератора (СГ), в теории синхронной машины в осях d-q, принято понимать: изображающий вектор тока статора, изображающий вектор напряжения статора, изображающий вектор тока возбуждения, изображающие вектора потокосцепления и их модули. Добавим к этому мгновенную мощность трехфазной системы, мгновенную реактивную мощность [2], мгновенные углы между изображающими векторами и осями d-q, В данной статье термин реактивная, мгновенная мощность определяет мгновенную электромагнитную энергию, запасенную трехфазным потребителем, с коэффициентом пропорциональности равным удвоенной угловой частоте вращения. Иногда, достаточно редко, изображающий вектор называется вектором пространственной волны тока, напряжения, э.д.с, потокосцепления и т.д. Все, перечисленные выше параметры, являются мгновенными величинами в функции времени.

Необходимость создания математической модели СГ в обобщенных параметрах обусловлена тем, что модули изображающих векторов тока I_m и напряжения U_m, мгновенная мощность p(t), мгновенная реактивная мощность q(t) достаточно просто схемотехнически определяются на практике, тем самым легко проверяется соответствие принятой модели реальному событию.

Рассмотрим принятую систему координат (рис. 1). В качестве неподвижных на плоскости координат возьмем симметричные фазные оси А, В. С, сдвинутые относительно друг друга на 120 эл. градусов, в центре пересечения этих осей находиться ось ротора СГ, относительно которой ротор вращается против часовой стрелки с переменной скоростью ω(t).

 

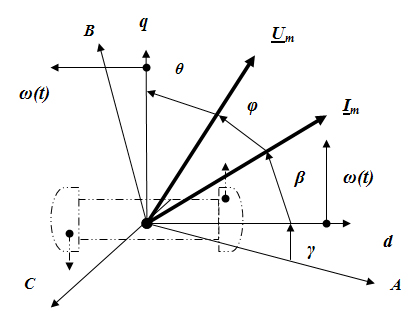
Рис. 1. Принятая система координат и направления осей.

 

Вместе с ротором вращаются оси d и q, закрепленные на роторе. Между осью А и осью d отсчитывается угол γ. Также с ротором, угловая скорость вращения которого), в общем случае, не является постоянной, вращаются изображающие вектора тока I_m и напряжения U_m, которые меняют положение относительно осей d и q за счет изменения во времени углов θ, φ, β:

θ(t) – мгновенный угол между изображающим вектором напряжения и поперечной осью ротора, отчитываемый от вектора напряжения в сторону поперечной оси, так называемый внутренний угол машины;

φ(t) – мгновенный угол между изображающими векторами тока и напряжения, так называемый угол нагрузки, отчитываемый от вектора тока в сторону вектора напряжения;

β(t) – мгновенный угол между продольной осью и изображающим вектором тока отчитываемый от продольной оси в сторону изображающего вектора тока.

Отметим, что изображающие вектора тока и напряжения, вращаясь вместе с ротором, не будучи «жестко» связанны с осями q и d, в каждый текущий момент времени определяют фазные токи и напряжения следующим образом:

u_a = U_m cos(γ + β + φ),

u_b = U_m cos(γ + β + φ - 120),

 u_c = U_m cos(γ + β + φ + 120),                                                                                 (1)

i_a = I_m cos(γ + β ),

i_b = I_m cos(γ + β - 120),

i_c = I_m cos(γ + β + 120).

Также примем во внимание, что для трехфазной симметричной системы всегда действуют выражения:

 i_a + i_b + i_c = u_a + u_b + u_c = Ψ_a + Ψ_b + Ψ_c = 0                                                          (2)

Из теории электрических машин известно, что изображающий вектор – это сумма векторов фазных статорных проекций, и он может быть записан как:

V_m= (2/3)( v_a + v_b exp120j + v_c exp240j); (3)

А модуль изображающего вектора может быть определен как:

V_m=(V_d+ V_q)^0,5 = (( v²_a + v²_b +v²_c )2/3)^0,5                                                                                        (4)

где: V_d ,V_q - проекции соответствующих изображающих векторов на оси d и q.

В соответствии с (3) изображающие вектора для трехфазного тока, напряжения, потокосцепления можно записать как:

I_m = I_m expj(γ + β),

U_m = U_m expj(γ + β + φ),

p(-Ψ_m ) = U_m expj(γ + β + φ) + rI_m expj(γ + β)                                                        (5)

где r – активное сопротивление статорной обмотки, Ψ_m – изображающий вектор потокосцепления статора, p = d / dt – оператор дифференцирования.

Чтобы определить производную по времени от изображающего вектора потокосцепления определим для начала выражения для потокосцеплений фазных контуров и контура возбуждения без учета успокоительных контуров:

Ψ_a = L_a i_a + M_ab i_b + M_ac i_c + M_af i_f ,

Ψ_b = L_b i_b + M_ba i_a + M_bc i_c + M_bf i_f ,                                                             (6)

Ψ_c = L_c i_c + M_ca i_a + M_cb i_b + M_cf i_f ,

Ψ_f = L_f i_f + M_af i_a + M_bf i_b + M_cf i_c .

Коэффициенты взаимоиндукции фазных обмоток между собой и взаимоиндукции фазных обмоток с обмоткой возбуждения, определяются следующим образом:

M_ab = M_ba = M_o + M_mcos (2γ – 120),

M_bc = M_cb = M_o + M_m cos 2γ ,

M_ac = M_ca = M_o + M_m cos (2γ + 120),

M_af = - M_f cos γ,

M_bf = - M_f cos (γ – 120),

M_cf = - M_f cos (γ + 120),

здесь: M_o – среднее значение коэффициента взаимоиндукции фазных обмоток, M_m – максимальный значение коэффициента взаимоиндукции фазных обмоток, M_f – максимальное значение коэффициента взаимоиндукции фазной обмотки и обмотки возбуждения при совпадении магнитных осей.

Коэффициенты самоиндукции фаз статора L_a , L_b , L_c определяются следующим образом:

 L_a = L_o + L_m cos 2γ,

 L_b = L_o + L_m cos (2γ + 120),

 L_c = L_o + L_m cos (2γ - 120),

гдe: L_o – среднее значение коэффициента самоиндукции фазных обмоток статора, L_m – максимальный коэффициент самоиндукции фазных обмоток статора.

Приведенные выше коэффициенты взаимоиндукции и самоиндукции подставим в (6) и после несложных тригонометрических преобразований полученные выражения уже подставим в (3), что позволит определить выражение для изображающего вектора потокосцепления синхронной машины [1]:

Ψ_m = I_m ((L_o – M_o )exp(j(γ + β)) + 1,5M_m expj(γ - β)) – M_f i_f expjγ,

или

Ψ_m = (L_o – M_o) I_m - M_f i_f +1,5M_m I_m exp(-j2β),

Ψ_f = L_f i_f - 1,5 M_f I_m cos β

где i_f = i_f expjγ - изображающий вектор тока возбуждения.

Теперь возьмем производную от изображающего вектора потокосцепления и подставим в (5), в результате получим комплексное уравнение синхронного генератора в обобщенных величинах:

U_m expj(γ + β + φ) + rI_m expj(γ + β) = M_f i_f γ ¹expj(γ +90) + M_f i_f¹expjγ - I¹_m ((L_o – M_o)exp(j(γ +β)) +1,5M_m expj(γ - β)) - I_m((L_o – M_o)(γ ¹+ β ¹)expj(γ + +β+90)+1,5M_m (γ ¹- β ¹)expj(γ – β + 90))                                                                               (7)

где: γ¹ – производная по времени от угла γ¹ = ω, I¹_m – производная по времени от модуля изображающего вектора тока, β¹- производная угла β по времени, i_f ¹- производная по времени тока возбуждения синхронной машины.

Выражение (7) представляет собою общее, комплексное уравнение СГ, записанное в физических параметрах. Это выражение не является переходом от трехфазной машины к двухфазной, но позволяет перейти к известным уравнениям Горева-Парка. представляющим собою проекцию выражения (7) на оси d-q. . Для получения уравнений Горева-Парка, исходное уравнение (7) спроецируем на оси d и q, для чего сократим левую и правую части на exp(jγ):

U_mexpj(β+φ)+ rI_mexp(jβ) = M_f i_f ωexp(j 90) + M_f i_f¹ - I¹_m((L_o – M_o)exp(jβ) + 1,5 M_mexpj(- β))- I_m((L_o – M_o)(ω + β ¹)exp[j(β+90))+1,5 M_m(ω - β ¹ )expj(90-β))

Теперь учтем некоторые соотношения при определении действительной и мнимой части полученного уравнения:

U_m sin(β + φ) = U_q,,

U_m cos(β + φ) = U_d,

I_m sinβ = I_q ,

I_m cosβ = I_d ;

(L_o – M_o) +1,5 M_m = L_d,

(L_o – M_o) - 1,5 M_m = L_q ,

где: L_d, L_q - реактивности по продольной и поперечной оси.

Используя эти соотношения, получим:

U_m cos(β+φ) = M_f i_f¹ - rI_mcosβ - I¹_m((L_o – M_o)cosβ + 1,5 M_m cos β) - -I_m ((L_o – M_o)(ω + β ¹)sin(-β)) + 1,5M_m(ω - β ¹)sinβ)

или после преобразований

U_d = -rI_d + M_f i_f¹ – I_d¹ L_d + ω L_q I_q

U_m sin(β+φ) = M_f i_f ω - rI_m sinβ - I¹_m((L_o – M_o)sinβ - 1,5M_m sinβ) - I_m ((L_o – M_o)(ω + β ¹)cosβ + 1,5M_m(ω - β ¹ ) cosβ )

или после преобразований

U_q = M_f i_f ω - rI_q - I_d L_d ω– I_q¹ L_q

Очевидно, что уравнения Горева-Парка являются частным случаем общего, комплексного уравнения синхронного генератора.

Теперь спроецируем комплексное уравнение СГ (7) на направление вектора трехфазного тока, для этого его левую и правую часть сократим на

expj(γ + β),

U_m expjφ + rI_m = M_f i_f ωexpj(90 -β) + M_f i_f¹exp(- j β) - I¹_m ((L_o – M_o) + +1,5M_mexpj(-2β))- I_m((L_o–M_o)(ω + β¹)expj90 +1,5M_m(ω - β ¹)expj(90–2β))

Выделим мнимую и действительную часть полученного выражения:

U_mcosφ = M_f i_f ω sinβ+M_f i_f¹сosβ – rI_m – I¹_m ((L_o–M_o) +1,5M_mcos2β) - 1,5M_m I_m (ω - β ¹)sin2β

U_msinφ = M_f i_f ω cosβ – M_f i_f¹sinβ – I_m (L_o–M_o)( ω + β¹) +1,5M_m I_m(ω - β¹) cos2β + 1,5M_m I¹_m sin2β                                                                                                              (8)

Преобразуем первое уравнение, используя известные в теории машин соотношения, приведенные выше при определении действительной и мнимой части выражения (7). В результате получим следующее:

U_mcosφ = M_f i_f ω sinβ+M_f i_f¹сosβ – rI_m – 0,5 I¹_m (L_q sin²β +L_d cos²β) - 0,5 I_m (L_d –L_q) (ω - β ¹)sin2β                                                                                                                             (9)

Умножим полученное уравнение на величину модуля изображающего вектора тока, затем преобразуем и получим выражение для мгновенной трехфазной мощности, потребляемой сетью:

2/3 p(t) = U_m I_m cosφ = M_f i_f ω I_m sinβ +M_f i_f¹ I_m сosβ – rI²_m - 0,5ω I²_m (L_d – L_q) sin2β - 0,5( L_d (I²_m сos²β)¹ + L_q (I²_m sin²β )¹ )

или

2/3 p(t) = U_d I_d + U_q I_q= M_f i_f ω I_q +M_f i_f¹ I_d – r(I²_d + I²_q ) - ω I_q I_d (L_d –L_q) - 0,5 (L_d(I²_d )¹ + L_q(I²_q )¹)                                                                                                                                                                      (10)

Очевидно, что электромагнитная энергия взаимодействия полей ротора и статора (первые два слагаемых в (9)) расходуется на нагрев обмоток статора (третье слагаемое), на пополнение запасенной электромагнитной энергии в статорных обмотках (пятое слагаемое), на потребление трехфазной сетью.

Теперь повторим похожую процедуру для второго уравнения в (8).

U_m sinφ = M_f i_f ω cosβ – M_f i_f¹sinβ + 0,5(L_d – L_q) I¹_m sin2β  - ω I_m(L_q sin²β + L_d cos²β) - β¹ I_m(L_d sin²β + L_q cos²β).                                                                                                           (11)

Мгновенную трехфазную, реактивную мощность определим следующим образом [2]:

2/3 q(t) = U_q I_d - U_d I_q

2/3 q(t) = U_m I_m sinφ = M_f i_f ω I_m cosβ – M_f i_f¹ I_m sinβ + 0,5(L_d – L_q) I_m I¹_m sin2β - ω I²_m(L_q sin²β + L_d cos²β) - β¹ I²_m(L_d sin²β + L_q cos²β),

или после преобразований:

2/3 q(t) =M_f i_f ω I_d –M_f i_f¹ I_q + L_d I¹_d I_q – L_q I¹_q I_d - ω (L_q I²_q + L_d I²_d )                    (12)

Мгновенная реактивная мощность, как видно из выражения (12), это результат электромагнитного взаимодействия ротора и статора (первые два слагаемых), изменение энергии взаимодействия статорных обмоток (третье и четвертое слагаемое), мгновенная электромагнитная энергия, накопленная в статорных обмотках, умноженная на двойную угловую частоту (пятое слагаемое).

Запишем теперь уравнения (9), (10), (11), (12) для установившегося режима:

U_m cosφ = M_f i_f ω sinβ– rI_m - 1,5M_m I_m ω sin2β,

или

U_m cosφ = M_f i_f ω sinβ – rI_m – 0,5 I_m ω (L_d –L_q) sin2β,

2/3 p(t) = M_f i_f ω I_m sinβ – rI²_m - 0,5ω I²_m (L_d – L_q) sin2β

или

2/3 p(t)= M_f i_f ω I_q – r(I²_d + I²_q ) - ω I_q I_d (L_d –L_q)_,

U_m sinφ = M_f i_f ω cosβ – I_m (L_o–M_o)ω +1,5M_m I_m ω cos2β,

U_m sinφ = M_f i_f ω cosβ - ω I_m(L_q sin²β + L_d cos²β).

2/3 q(t) =M_f i_f ω I_d - ω (L_q I²_q + L_d I²_d )                                                                    (13)

Определим теперь запасенную энергию в контурах СГ, которая определяется как половинная сумма произведений соответствующих мгновенных потокосцеплений на соответствующие токи

W_э = 0,5 (Ψ_a i_a + Ψ_b i_b+ Ψ_c i_c + Ψ_f i_f )

Преобразуем это выражение, используя (6) и (1) в следующее:

W_э = 0,5 (1,5 I²_m ((L_o-M_o) + 1,5M_m cos2β) - 3 M_f i_f I_m cosβ + L_f i²_f ),

W_э = 1,5(0,5L_q I²_m sin²β + 0,5L_d I²_m cos²β) – 1,5M_f i_f I_d + 0,5L_f i²_f ,

W_э = 1,5 (0,5L_q I²_q + 0,5L_d I²_d ) -1,5 M_f i_f I_d + 0,5 L_f i²_f (14)

Определим теперь электромагнитный момент как производную от энергии магнитных полей по углу поворота ротора

M_э = d(W_э)/d γ

Произведем дифференцирование Wэ по углу поворота ротора γ, учитывая, что d( I²_m )/dγ = 0, d( L_f i²_f )/dγ = 0,

M_э = d( W_э )/dγ = 1,5 M_f i_f I_m sinβ – 2,25M_m I²_m sin2β

M_э = d( W_э )/dγ = 1,5 M_f i_f I_m sinβ – 0,75(L_q + L_d ) I²_m sin2β                                  (15)

Напряжение обмотки возбуждения определим следующим образом:

u_f = L_f i¹_f -1.5 M _f (I _m cosβ)¹ + r_f i_f (16)

Выражения (9), (11), (15), (16) являются уравнениями СГ в обобщенных параметрах.

Предложенное комплексное уравнение синхронной машины в обобщенных величинах (7) не представляет собою переход от трехфазной машины к двухфазной. В частном случае это выражение позволяет перейти к известным уравнениям Горева-Парка. Для перехода к фазным величинам достаточно спроецировать изображающие вектора трехфазного напряжения и тока на фазные оси (1). Поскольку характер изменения модуля изображающего вектора напряжения определяет форму кривых мгновенных фазных напряжений [3], то имеет смысл при расчетах цепей с нелинейной нагрузкой определять модули изображающих векторов тока I_m и напряжения U_m,, мгновенные углы θ, φ, β, для последующего определения фазных напряжений u_abc и токов i_abc\. c помощью (1).

 

Литература

 

1.                  Бондаренко А.Е. Регулирование судовых генераторных агрегатов по мгновенным значениям параметров режимов. Дисс. на соискание ученой степени к.т.н. 186 стр., СПбГМТУ, Санкт-Петербург 1992г.

2.                  Бондаренко А.Е., Вилесов Д.В. Мгновенная активная, реактивная, полная мощность, эффективность энергопотребления в трехфазных сетях. Журнал научных публикаций аспирантов и докторантов. N10(64), октябрь 2011, стр. 94-98, Курск.

3.                  Бондаренко А.Е., Вилесов Д.В. Оценка качества трехфазного напряжения по модулю изображающего вектора. Журнал научных публикаций аспирантов и докторантов. N11(65), ноябрь 2011, стр. 100-188, Курск.

 

Поступила в редакцию 13.11.2013 г.