Моделирование методом Монте-Карло процесса радиационного распухания в конструкционных материалах

 

Царина Анна Георгиевна,

кандидат физико-математических наук, доцент,

Колганов Константин Михайлович,

старший преподаватель,

Кочкарева Яна Викторовна,

аспирант.

Обнинский институт атомной энергетики – филиал Национального исследовательского ядерного университета МИФИ.

 

Работа выполнена при поддержке РФФИ (грант № 11-08-00905-а).

 

Введение

 

Общеизвестно, что под воздействием радиационного облучения происходит изменение структуры материала, что отражается на его свойствах, таких как прочность, пластичность, вязкость, текучесть и т.д. В зависимости, с одной стороны, от характеристик материала (строения его кристаллической решетки, его химического состава) и, с другой стороны, от параметров облучения (дозы, температуры) развиваться разные процессы, связанные с появлением и развитием структурных дефектов и приводящие, в итоге, к таким явлениям как распухание, охрупчивание и уплотнение.

В аустенитных сталях и сплавах при высокотемпературном нейтронном облучении образуются и растут вакансионные поры, при этом междоузельные атомы, обладающие большой подвижностью, уходят на стоки[1]. Это является причиной увеличения объема металла, то есть радиационного распухания.

Современные задачи радиационного материаловедения требуют исследования процессов, происходящих в материалах под облучения, что практически невозможно без математического моделирования, позволяющего заменить реальный эксперимент.

Многоуровневый подход к построению таких моделей позволяет описать весь сложный процесс распухания от появления первичных дефектов до непосредственно количественной оценки распухания образца материала. Обычно выделяют три уровня: микроуровень (повреждения на уровне отдельных атомов, образование точечных дефектов), мезоуровень (комплексы дефектов, зарождение плоскостных и объемных дефектов) и макроуровень (эволюция объемных дефектов). При такой схеме на каждом из низших уровней формируется информация, являющаяся исходной для следующего.

Предлагаемый подход позволяет моделировать на макроуровне явления, вызванные облучением определенного материала, прогнозируя возможные сценарии образования и развития трехмерных дефектов – кластеров вакансий и вакансионных пор. Таким образом, рассматривается эволюция системы, состоящей из образца заданного материала с появляющимися в нем объемными радиационными дефектами.

 

Описание математической модели

 

Если рассматриваемая система включает в себя набор разноразмерных подвижных включений, то ее состояние в некоторый момент времени можно описать функцией распределения этих включений по размерам. Для рассматриваемого процесса распухания можно выделить два механизма, приводящих к изменению размеров дефектов (включений): коалесценция вакансионных пор и флуктационные изменения размера за счет стохастической диффузией точечных дефектов в объеме материала.

Первый механизм может быть описан уравнением коагуляции М. Смолуховского:

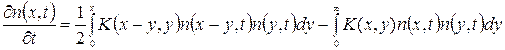,  (1)

где n(x,t) – концентрация в системе «частиц» размера x в момент времени t

Ядро коагуляции K(x,y) описывает интенсивность коагуляции частиц размера x и y соответственно.

Второй механизм – изменение размеров за счет диффузии точечных дефектов к поверхности объемных – может быть описан уравнением вида уравнения Фоккера-Планка.

В классическом виде уравнение Фоккера-Планка приведено для функции распределения частиц по импульсам и описывает эволюцию в процессах, где важна стохастическая природа явления[2]:

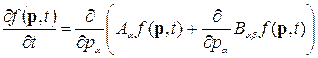,                                                 (2)

где  и  определяются через средние характеристики столкновений, а именно:

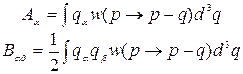                                                                     (3)

 - отнесенная к единице времени вероятность изменения импульса со значения p на значение q до значения p-q.

Это уравнение может быть обобщено на другие измеримые параметры системы, такие как размер, масса и так далее.

Соответственно, функцию распределения в уравнении (2) необходимо интерпретировать как функцию распределения дефектов по размерам. Данное кинетическое уравнение показывает, что флуктуации размеров частиц в своей интегральной составляющей оказывают существенное влияние на состояние системы в целом.

 

Имитационная трехмерная модель процесса распухания

 

Процесс образования и роста в системе радиационно-индуцированных кластеров вакансий и пор можно схематично представить в виде следующего алгоритма:

1.                  Смещение под воздействием налетающих частиц атомов из узлов кристаллической решетки и образование пар вакансия-междоузлие.

2.                  Формирование каскадов смещений.

3.                  Образование комплексов дефектов (кластеры вакансий и междоузлий).

4.                  Структурная перестройка существующих в системе дефектов, образование вакансионных пор.

5.                  Образование объемных скоплений дефектов в виде вакансионных пор приводит к распуханию материала[3].

Интенсивность этого процесса для конкретного материала зависит от вида и характеристик облучения: энергии налетающих частиц должно быть достаточно для формирования каскада, то есть для многократного разрыва межатомных связей и изменения положения атомов в кристаллической решётке при движении частицы в материале.

Каждый шаг приведенного выше алгоритма включает сложные процессы, происходящие на разных масштабах времени и пространства, и требует разных подходов к построению моделей. Моделирование в данной работе проводится на макроуровне, где предполагаются известными концентрация и характеристики распределения кластеров в пространстве и по размерам, подвижность и структура кластеров.

Имитационное моделирование методом Монте-Карло обладает рядом преимуществ, давая возможность описать эволюцию системы согласно известным феноменологическим законам. Современные вычислительные машины и относительная легкость распараллеливания алгоритмов метода статистических испытаний позволяют рассчитывать системы с большим количеством компонент.

Для решения поставленной задачи рассматриваем среду, представляющую из себя некий образец материала с зарождающимися в нем и растущими вакансионными порами. Считаем, что согласно экспериментальным данным[4] вакансионные поры имеют форму сферы. Таким образом, для описания механизма зарождения дефектов разыгрываем их появление в среде в соответствии с заданным законом распределения.

Тогда, например, при равномерном распределении по осям OX и OY и при нормальном распределении по высоте образца срез материала будет выглядеть следующим образом (рис. 1):

 

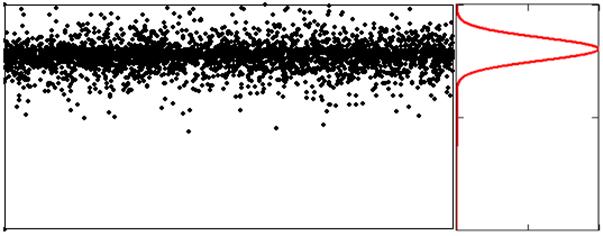
Рис. 1. Распределение 1000 дефектов, нормальное распределение по высоте, одна история ММК.

 

Если задать экспоненциальное распределение по высоте образца, то срез при тех же значениях остальных параметров будет выглядеть иначе (рис. 2).

 

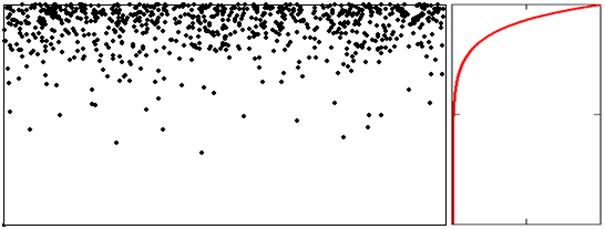
Рис. 2. Распределение 1000 дефектов, экспоненциальное распределение по высоте, одна история ММК.

 

Для того чтобы можно было моделировать процессы коалесценции и разрастания пор согласно уравнениям (1) и (2), каждому объекту системы были сопоставлены следующие свойства: координаты поры в трехмерном пространстве, радиус поры, скорость и направление миграции, скорость флуктационного роста кластера за счет присоединения к нему одиночных вакансий.

На начальном этапе t₀ в системе образуется N таких элементов (рис. 1, 2). Значение N определяется из заданной концентрации вакансионных кластеров.

Рассматриваем временной интервал от t₀ до t_M, где t_M - максимальное время наблюдения за системой. Каждый шаг эволюции системы состоит из нескольких этапов. В момент времен t_k, где  происходит рост всех вакансионных пор, содержащихся в образце с заданной скоростью. При этом определяются и новые координаты поры, если она подвижна. После того как изменились расположение и размеры объемных дефектов в системе, появляется вероятность, что некоторые из них оказались настолько близко друг к другу, что произойдет их слияние. Следовательно, заключительным этапом является коалесценция близко расположенных объектов.

 

Результаты моделирования

 

Предложенный подход позволяет при моделировании получать информацию о состоянии системы в любой момент времени, отслеживая поэтапную эволюцию структурных дефектов в материале.

Одна история метода Монте-Карло является иллюстрацией возможного развития процесса в диапазоне времен от t₀ до t_M. В разработанной программной реализации есть возможность сохранить в графический файл вид среза образца в любом разрешении (рис. 3).

 

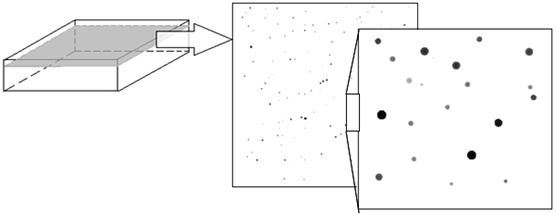
Рис. 3. Дефекты на срезе образца.

 

Как упоминалось выше, одним из показателей, позволяющим оценить степень изменений, происходящих в материале, является распределение по размерам дефектов, образовавшихся за некоторый промежуток времени. Для некоторых материалов известны полученные экспериментальным образом данные для разных значений температуры и повреждающих доз[5]. Разработанная программа, реализующая модель, позволяет получить результаты, согласующиеся с экспериментом. При проведении расчетов согласно эмпирически найденным закономерностям[6] изменяется скорость роста и диффузии включений по объему образца, а также начальные размеры пор для того чтобы корректно обеспечить зависимость от температуры и дозы. Для конкретного материала опытным путем подбираются значения для исходных данных.

Результаты моделирования представлены (рис. 4, 5) для стали ЧС-68⁶. По оси абсцисс указаны размеры вакансионных пор в нанометрах, по оси ординат – доля пор определенного размера.

 

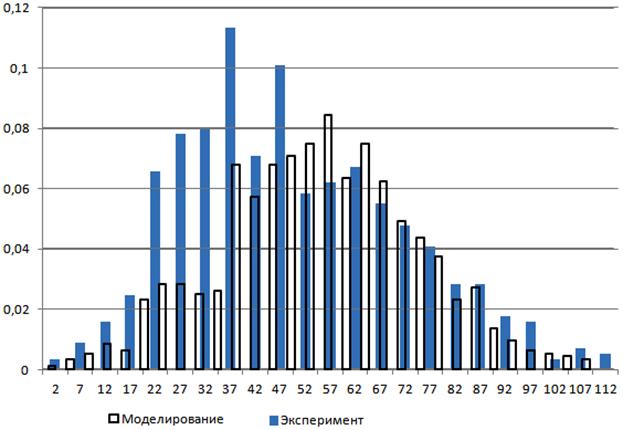
Рис. 4. Распределение пор по размерам (температура облучения 500⁰С).

 

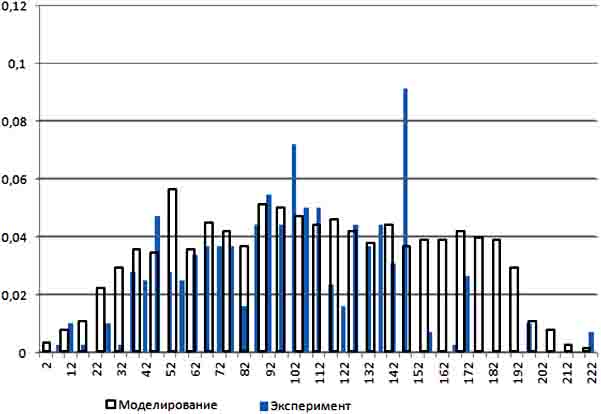
Рис. 5. Распределение пор по размерам (температура облучения 550⁰С).

 

Выводы

 

Разработана и реализована на программном уровне имитационная трехмерная модель образования и роста объемных дефектов в материале под воздействием облучения. Результаты вычислительных экспериментов хорошо согласуются с данными, полученными при исследовании реальных образцов конструкционных материалов.

 

Литература

 

1.                  Афонин В.К., Ермаков Б.С., Лебедев Е.Л. и др; под ред. Солнцева Ю.П. Металлы и сплавы: справочник. - СПб.: Профессионал; СПб.: Мир и Семья, 2003. - 1066 с.

2.                  Кальченко А.С., Брык В.В., Воеводин В.Н., Лазарев Н.П. Моделирование распухания стали Х18Н10Т в имитационных и реакторных условиях // Вопросы атомной науки и техники. Сер. Физика радиационных повреждений и радиационное материаловедение, №4-2, 2009, С. 131-139

3.                  Кирсанов В.В. Радиационные дефекты и связанные с ними эффекты // Соровский образовательный журнал, том 7, №10, 2001, С. 88-94.

4.                  Козлов В.А., Портных И.А. Условия достижения стадии стационарного радиационного распухания // Физика металлов и металловедение, том 103, №1, 2007, С. 108-112.

5.                  Лифшиц Е.М., Питаевский Л.П. Физическая кинетика (т. X). – М.: Наука. Гл. ред. aиз.-мат. лит., 1979. – 528 с.

6.                  Портных И.А., Козлов А.В. Связь скорости радиационного распухания с ростом и коалесценцией радиационных пор // Вопросы атомной науки и техники. Сер. Материаловедение и новые материалы. Вып. 2(71), 2008,С.3-13.

 

Поступила в редакцию 09.01.2013 г.