Место для кибернетики
Васильев Геннадий Федорович.
Известны динамические системы с отрицательной обратной связью, достигающие благодаря своим параметрам состояния равновесия, при котором некоторая выходная величина системы, называемая регулируемой величиной (далее, РВ), находится в состоянии стабилизации.
Эти системы состоят из исполнительного механизма (далее, ИМ) и формирователя закона управления (далее, ФЗУ). На выходе ИМ имеет место РВ, и эта величина поступает на вход ФЗУ, чем обеспечивается обратная связь. На выходе ФЗУ при этом формируется закон управления. Текущее значение закона управления представляет собой сигнал управления (далее, СУ), поступающий на вход ИМ, чем обеспечивается управление. Так замыкается система. Отрицательная обратная связь возникает, как следствие согласования статических характеристик ИМ и ФЗУ. В случае если ИМ имеет возрастающую статическую характеристику (рост СУ приводит к росту РВ), то ФЗУ должен иметь убывающую (рост РВ приводит к уменьшению СУ), и наоборот, если у ИМ убывающая статическая характеристика, то ФЗУ должен иметь возрастающую. Если все эти условия выполняются, то образуется упомянутая выше динамическая система с отрицательной обратной связью, имеющая возможность достичь состояния равновесия. В состоянии равновесия ИМ поддерживает такое значение РВ, при котором ФЗУ вырабатывает СУ, значение которого необходимо ИМ, для поддержания именно этого значения РВ.
Возможны ФЗУ параметрические и алгоритмические (терминология автора). В соответствии с этим возможны две модели управления: параметрическая и алгоритмическая, и этим моделям соответствуют два вида систем. В параметрической модели роль ФЗУ выполняет элемент системы. Статическая характеристика этого элемента и представляет собой закон управления для системы. В алгоритмической модели вводится дополнительный сигнал от системы верхнего уровня, называемый сигналом задания (далее, СЗ). При этом СУ системы формируется в соответствии с алгоритмом: СУ=СЗ-СОС, где СОС (сигнал обратной связи) это – либо непосредственно РВ, либо сигнал прямо пропорциональный РВ. Такое устройство ФЗУ позволяет системе верхнего уровня оперативно изменять закон управления, и тем самым управлять системой.
Не смотря на явное различие в устройстве параметрической и алгоритмической моделей, в сущности, параметрическая модель эквивалентна алгоритмической модели для некоторого фиксированного значения СЗ. Это позволяет, при необходимости, конвертировать параметрическую систему в эквивалентную ей алгоритмическую систему и обратно.
Таковы теоретические основы систем с отрицательной обратной связью, приведенные здесь для понимания дальнейшего изложения. Эта теория складывалась постепенно из многих фрагментов многие сотни лет, усилиями многих авторов, начиная с решения отдельных вопросов автоматизации до глубоких теоретических разработок, пока Норберт Винер (Wiener, 1948) не опубликовал свою книгу «Кибернетика или управление и связь в животном и машине» [3], которая положила начало новой науке – кибернетике. Объект науки – система с отрицательной обратной связью.
Это был революционный шаг, однако следует заметить, что Винер существенно сузил сферу приложения кибернетики, ограничив ее объектами техники и царства животных, не распространив ее на все объекты Вселенной. Исправление этого недостатка является целью настоящей статьи.
| Вот ГДЗ по геометрии 8 класс Атанасян вот www.euroki.org |
Известно, что материя обладает фундаментальным свойством – взаимодействием. Благодаря этому в природе возможно самопроизвольное возникновение систем, соответствующих описанным выше моделям. Один объект природы в этом взаимодействии играет роль ИМ, другой – ФЗУ. Возникшая стабильная система обогащает природу новым свойством, создающим дополнительные условия для возникновения новых систем. Так эволюционирует материя.
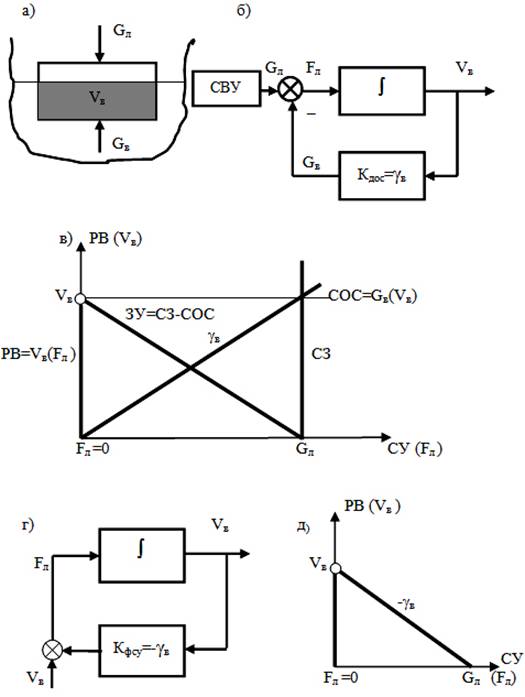
Рис. 1. Функциональные схемы и рабочие характеристики параметрической системы «лед-вода».
Чтобы проиллюстрировать процессы, происходящие в природных системах, проведем системный анализ на примере простейшей самоорганизующейся параметрической системы «лед-вода». Физическая модель системы показана на рис. 1, а. Индекс «л» относит величины к параметрам льда, а индекс «в» – к параметрам воды. В этой системе сила гравитации Gл погружают лед в воду, а возрастающий при этом объем вытесненной воды Vв создает противодействующую силу Gв.
Особенностью параметрических систем неживой природы является отсутствие специализированных элементов для передачи информации, что противодействует дифференциации элементов системы, делает систему «закрытой» и затрудняет ее анализ. Для преодоления этих трудностей, представим параметрическую систему в виде алгоритмической системы (см. рис. 1, б). Тогда сигналом задания (СЗ) от системы верхнего уровня (СВУ) будет вес льдины Gл. Сигналом обратной связи (СОС) будет вес вытесненной воды Gв, а сигналом управления (СУ) - избыточная сила льда, равная разнице между сигналом задания и сигналом обратной связи: Fл=Gл-Gв. Далее, регулируемой величиной (РВ), подлежащей стабилизации, будет объем вытесненной воды Vв. Датчиком обратной связи в этой условной системе будет преобразователь объема воды в вес. Его коэффициент передачи – есть удельный вес воды, т.о. Кдос=gв.
В прямой цепи (в ИМ), преобразующей избыточную силу в объем вытесненной воды, происходит ряд последовательных преобразований. Рассмотрим этот ряд от конца к началу:
1) объем вытесненной воды Vв определяется глубиной погружения льда;
2) глубина погружения льда есть интеграл по времени от скорости погружения центра инерции льдины во время углубления;
3) скорость центра инерции льдины есть следствие количества движения льдины;
4) количество движения есть интеграл по времени от приложенной избыточной силы льда (Fл).
Таким образом, ИМ представляет собой интегратор, и значение РВ на его выходе зависит не только от значения СУ на входе, но и возрастает во времени при наличии даже малейшего рассогласования. Кроме того, у воды отсутствует сила трения покоя. Все это неизбежно приводит систему к нулевому СУ в состоянии равновесия. Следовательно, статическая характеристика ИМ совпадает с координатной осью РВ.
Построим рабочую характеристику алгоритмической системы. По оси РВ откладываем вытесненный объем воды Vв, по оси СУ – силу, действующую на льдину. Наносим на график СОС=Gв=f(Vв)=gв*Vв, где gв – удельный вес воды. Наносим на график СЗ=const, как перпендикуляр к оси СУ из точки, соответствующей весу льдины Gл. Построим характеристику закона управления ЗУ=СЗ-СОС. Статическая характеристика ИМ, представляющего собой интегратор, совпадает, как уже было отмечено, с осью регулируемой величины Vв. Ее пересечение с характеристикой закона управления даст точку равновесия системы (координаты: рв=Vв; су=Fл=0). Рабочая характеристика алгоритмической системы показана на рис. 1, в. Формирователь закона управления (ФЗУ) этой системы состоит из виртуальной системы верхнего уровня (СВУ), виртуального датчика обратной связи и виртуального узла сравнения сигналов СЗ и СОС.
Но физически наша система остается параметрической системой, поэтому закон управления - это, конечно, статическая характеристика параметрического ФЗУ (Кфзу=-gв). Полученная в результате функциональная схема нашей параметрической системы показана на рис. 1, г, а ее рабочая характеристика – на рис. 1, д. Эти данные полностью описывают рассмотренную систему.
Чтобы появился водоем и льдина, необходима планета. Рассмотрим систему «звезда-планета». Известны объекты природы, например, звезда и некоторый достаточно массивный космический объект. Если этот космический объект имеет достаточно сильный гравитационный контакт со звездой, то звезда «захватывает» объект, объект начинает вращаться вокруг звезды, и образуется стабильная параметрическая система. Инерция космического объекта сохраняет его линейную скорость в пространстве. Вследствие этого, при приближении к звезде частота оборотов увеличивается и возрастает центробежная сила, удаляющая объект от звезды. При удалении, наоборот, центробежная сила уменьшается. Система приходит в равновесие при определенном расстоянии между центрами масс звезды и объекта, при котором сила притяжения равна центробежной силе. Космический объект становится планетой этой звезды со всеми вытекающими из этого последствиями. Если бы данная звезда и данный космический объект не находились бы в описанном выше контакте, то расстояние между ними не стабилизировалось бы и описанная система не возникла бы, а космический объект в планету не превратился бы. Т.е. возникшая система это некоторая материальная сущность, отличающаяся от суммы входящих в нее элементов.
Таких примеров можно привести бесчисленное множество, т.к. все природные объекты контактируют друг с другом и образуют стабильные системы – явления природы, которые по мере усложнения образуют все более сложные системы. А отдельных, ни с чем не связанных материальных элементов во Вселенной, вообще, не существует.
И главное заключение – система, возникшая из природных объектов, сама является объектом (явлением) природы, т.к. проявляется в природе свойствами, которых нет у суммы, входящих в эту систему элементов.
Таким образом, каждая система является ступенькой в поступательном развитии (эволюции) материи. По мере усложнения появляются и ступеньки живой материи. Это значит, что живая материя – это система с новыми свойствами. И, если предположить, что объектами природы являются лишь элементы системы, а сама система не является объектом природы, то живая материя – не объект природы. Но это – абсурд, доказывающий, что последнее предположение ложно. Кроме того, если рассмотреть каждый элемент системы, то окажется, что и сам этот элемент тоже – система. Все это говорит о том, что объект кибернетики является природным явлением.
Эволюция материи, осуществляемая самоорганизацией систем, приводит к появлению человека, который не подозревает о системах – природных явлениях. Человек просто «открывает» систему и использует ее в технике. При этом под системой, как правило, понимается система, построенная по алгоритмической модели, т.к. в технике любое устройство должно подчиняться человеку, как системе верхнего уровня. Винер, положив начало кибернетики, также имел в виду именно алгоритмическую модель. И хотя Винер предполагал, что кибернетика охватит и животный мир, отсутствие параметрической модели тормозит практическое развитие биокибернетики, т.к. в живой природе наиболее распространенной является именно параметрическая модель управления (Г.Ф. Васильев, 2013), [2]. Из алгоритмических моделей в живой материи на сегодняшний день пока открыта лишь система управления двигательной единицей в организме млекопитающих (Г.Ф. Васильев, 2013), [1].
Из всего сказанного следуют выводы:
1. Каждый объект Вселенной, за исключением элементарных частиц, является системой с отрицательной обратной связью.
2. Система с отрицательной обратной связью является научным объектом кибернетики.
3. Кибернетика является естественной наукой.
Таким образом, для обеспечения гармоничного развития всего естествознания, кибернетика должна быть отнесена к естественным наукам. Кибернетика дает правильное осмысление природных явлений, объясняет процесс эволюции материи, дает прогнозы развития материи.
В случае включения кибернетики в группу естествознания, можно было бы предложить следующую классификацию для естественных наук (см. рис. 2).
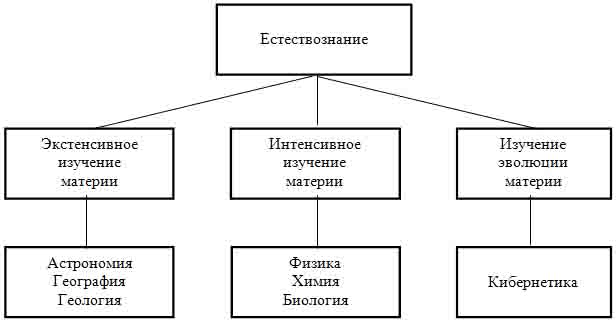
Рис. 2. Классификация естественных наук.
Литература
1. Васильев Г.Ф., Явление саморегуляции двигательной единицы // Журнал научных публикаций аспирантов и докторантов, Курск. – 2013, - №3, - с. 160-164.
2. Васильев Г.Ф., Кибернетика и биология // Биофизика, 2013, том. 58, вып. 4, с. 732-736.
3. Винер Н., Кибернетика или управление и связь в животном и машине: перевод с англ. (Главная редакция изданий для зарубежных стран издательства «Наука», М., 1983).
Поступила в редакцию 20.08.2013 г.