Программное обеспечение для создания рисунков в редакторе Latex
Беженцев Роман Вадимович,
студент Комсомольского-на-Амуре государственного технического университета.
Данная работа посвящена разработке программного обеспечения, предназначенного для облегчения создания рисунков в среде LaTeX. Здесь описываются проблемы рисования изображений стандартными средствами LaTeX и основные принципы работы программы PaintTeX.
Введение
Как известно, для получения пользователем изображения в среде LaTeX предусмотрены команды, которые после компиляции текста пользователя выглядят в виде композиции примитивов, составляющих вместе готовый рисунок. О том, как создавать динамические рисунки писал Francesc Sunol [Francesc Sunol].
Проблема рисования в LaTeX, а также мотивация рисовать в нём, а не вставлять готовое изображение, хорошо описаны в диссертации Jie Xiao [Jie Xiao]. Поскольку процесс создания рисунков в редакторе LaTeX не является WYSIWYG («What You See Is what You Get» - «что Вы видите, то и получите»), а сводится к ручному набору команд вывода графики на языке TeX, пользователю приходится лишь представлять, как будет выглядеть готовый рисунок, а также приблизительно подбирать координаты опорных точек.
В данной работе описывается разработанное автором программное обеспечение PaintTeX, призванное для решения этой проблемы. Оно было разработано на языке C++ и WinAPI, с применением методов многопоточной обработки данных, что гарантирует высокую производительность работы программы. Для упрощения создания рисунков другими авторами также разрабатывались программные обеспечения Graphviz [Jie Xiao] для рисования графов, Drawlets [Jie Xiao] для рисования произвольных рисунков, а также FeynEdit [Hahn T.] и JaxoDraw [Binosi D.] для рисования диаграмм Фейнмана.
Вывод прямолинейного отрезка
Для вывода прямолинейного отрезка или вектора в тексте пользователя, помимо координаты опорной точки, приходится указывать ещё и угол наклона с помощью отношения ширины к высоте. В языке TeX команда вывода отрезка выглядит следующим образом:
\put(60,50){\line(1,-2){20}}
где (60,50) – координаты начальной точки отрезка, (1,-2) - угол наклона в виде соотношения длинны к высоте, 20 - длина проекции на ось $ОХ$. Значения в отношении, задающем наклон, не должны превосходить 6 по абсолютной величине у отрезков, и 4 у векторов, а также не должны иметь общих делителей, кроме 1. Подробности можно найти в книгах С. М. Львовского [Львовский С. М.] и Д. Е. Кнута [Кнут Д. Е.].
Созданное автором программное обеспечение PaintTeX предоставляет WYSIWYG интерфейс для рисования изображения с помощью примитивов, а затем преобразует каждый примитив в соответствующую команду вывода графики на языке TeX. Например, чтобы нарисовать изображение, показанное на рисунке 1, нужно долгое время рассчитывать координаты опорных точек и другие параметры команд вывода графики для каждого примитива, или подгонять их приблизительно. Данный рисунок был нарисован в программе PaintTeX, код вывода следующий:
\begin{picture}(215,283)
\qbezier(99,172)(105,172)(112,172)
\qbezier(112,172)(108,174)(105,175)
\qbezier(112,172)(108,171)(105,169)
\qbezier(63,193)(82,170)(102,147)
\qbezier(102,147)(100,151)(99,155)
\qbezier(102,147)(98,149)(95,151)
\qbezier(0,14)(111,14)(209,14)
\qbezier(209,14)(205,16)(202,17)
\qbezier(209,14)(205,13)(202,11)
\qbezier(168,22)(89,129)(8,234)
\qbezier(8,22)(93,22)(168,22)
\qbezier(8,234)(8,128)(8,22)
\qbezier(0,13)(0,145)(0,276)
\qbezier(0,276)(-1,273)(-3,269)
\qbezier(0,276)(1,273)(3,270)
\put(64,192){\circle{38}}
\put(101,160){V}
\put(8,2){O}
\put(10,283){Y}
\put(215,0){Х}
\end{picture}
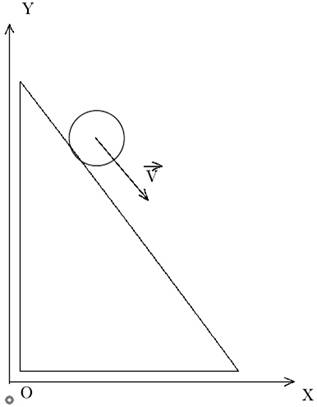
Рис. 1. Пример рисунка в LaTeX.
Рассмотрим PaintTeX в действии. Пользователь выбирает желаемый примитив и рисует его, указывая координаты опорных точек, по которым программа рисует примитив и сохраняет их в памяти. При сохранении рисунка программа вставляет в файл текст команды вывода примитива с сохранёнными координатами опорных точек. Сложные примитивы выводятся в виде композиции более простых примитивов, например вектор – это 3 прямых отрезка, соеденённых концами в одной точке, что образует стрелку, а прямоугольник – 4 прямых отрезка. Таким методом можно выводить огромное множество фигур, включая и трёхмерные.
Принцип работы программы
Принцип работы разрабатываемой программы состоит в следующем. При запуске программы появляется окно с меню, панелью инструментов и областью для рисования. Пользователь выбирает примитив на панели инструментов, а затем курсором мыши задаёт координаты опорных точек. Координаты опорных точек сохраняются в экземпляре класса выбранной фигуры и по ним рисуется сам примитив. При выборе пункта меню «Сохранить», программа сохраняет команды вывода примитивов в файл результатов, вставляя необходимые параметры (координаты, радиус) из координат опорных точек.
Под каждый примитив в программе выделяется объект класса для данного примитива. В ходе текущей стадии разработки существует 7 классов: VETREX, LINE, LABEL, BIZE, SQVR, CIRKLE, FISH. Каждый из этих классов является дочерним от базового класса FIGURE. Содержание класса FIGURE следующее:
class FIGURE
{
public:
POINT *pt;
FIGURE *nextFig;
virtual void print() = 0;
};
Благодаря механизму наследования, каждый дочерний класс наследует от базового указатели типов POINT, FIGURE и виртуальную функцию print(). При создании примитива запускается функция инициализации, которая преобразовывает указатель *pt в массив точек необходимой размерности для заданного примитива. То есть, если создаётся отрезок, в конструкторе LINE срабатывает команда pt = new POINT[2], а если прямоугольник - pt = new POINT[4] в конструкторе SQVR. Указатель *nextFig служит для формирования стека примитивов. Благодаря механизму наследования он может указывать на любой класс примитива.
В каждом описании классов примитивов по-своему переопределена функция вывода print(). Эта функция отвечает за вывод команды рисования примитива в текстовый файл, из которого набор этих команд можно копировать в статью и скомпилировать средствами LaTeX. В каждом классе данная функция выводит в файл собственную команду и параметры, содержащиеся в выбранном объекте. Ниже для примера приведено содержание класса примитивов «метка»:
class LABEL : public FIGURE
{
public:
char *lab;
void ini (int x, int y, char *str, int len, HDC hdc)
{
pt = new POINT;
pt[0].x = x;
pt[0].y = y;
lab = new char[len+1];
strcpy(lab, str);
TextOutA(hdc, pt->x, pt->y, lab, strlen(lab));
}
LABEL ()
void print()
{
ofile << "\\put(" << pt[0].x - Canv_left << ","
<< Canv_top - pt[0].y << "){" << lab << "}" << endl;
}
}*label;
Этот класс содержит указатель *lab, который преобразуется в строку для хранения текста метки, функцию инициализации, которая сохраняет данные в структуре и рисует текст, функцию print(), преобразующую рисунок в команды вывода графики с учётом кадрирования, и указатель *label, отвечающего за работу стека. Функция создания примитива «метка» выглядит следующим образом:
LABEL *new_label(int x, int y, char *str, int len, HDC hdc)
{
LABEL *label_new = new LABEL;
label_new->ini(x, y, str, len, hdc);
if (!labelcount++) label_new->nextFig = 0;
else label_new->nextFig = label;
return label_new;
}
Когда пользователь рисует примитив, в данном случае метку, функции создания передаются координаты опорной точки, строка текста, длина строки и дескриптор устройства, куда будет рисоваться текст. Поскольку для каждого нового примитива память выделяется динамически, то для инициализации пришлось использовать функцию инициализации, а не конструктор.
При сохранении команд, программа на каждый класс примитива создаёт отдельный поток. Каждый поток запускает функцию, которая при помощи мютекса синхронизирует вывод каждой команды. Объявление данной функции следующее.
void save(FIGURE *curfig, int counter)
Как видим, аргумент *curfig – указатель на стек примитивов, а counter - их общее количество. Благодаря механизму наследования, каждый класс примитива является классом FIGURE, а значит, для синхронного вывода примитивов любого класса достаточно использовать одну функцию. Так же, благодаря виртуальной функции print(), при помощи curfig->print(); можно обращаться к функции вывода каждого примитива, а программа уже будет знать, какой именно примитив надо вывести в файл.
Математические модели были взяты из книги «Математические основы машинной графики»[Роджерс Д.]. Например, Кривая Безье — параметрическая кривая, задаваемая выражением
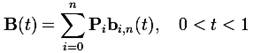
где Pi — функция компонент векторов опорных вершин, а bi,n(t) — базисные функции кривой Безье, называемые также полиномами Бернштейна.
Поскольку синтаксис языка TeX позволяет выводить кривые только по трём точкам, формула для их вывода была упрощена.
X = (1-t) * (1-t) * pt[0].x + 2*t*(1-t)*pt[1].x + t*t*pt[2].x;
Y = (1-t) * (1-t) * pt[0].y + 2*t*(1-t)*pt[1].y + t*t*pt[2].y;
где pt[0].x, pt[1].x, pt[2].x - координаты опорных точек по оси OX, а pt[0].y, pt[1].y, pt[2].y - координаты опорных точек по оси OY. При построении кривой, программа с шагом t = t + 0.01 находит точки, расположенные на кривой, и затем соединяет их маленькими отрезками.
Проблемы в ходе реализации программного обеспечения.
В ходе работы над программным обеспечением появились следующие проблемы. Поскольку значения, отвечающие за наклон в примитивах «отрезок» и «вектор» должны быть целыми, и их количество сильно ограничено, то для наклона примитива существует ограниченное количество углов. В разрабатываемом программном обеспечении пользователь рисует отрезки и векторы, задавая координаты начальной и конечной точки. Конвертировать их координаты в команду вывода на языке TeX не удалось, поэтому для вывода прямых линий было решено использовать кривые Безье, определяя начало линии, середину и конец. Поскольку для вывода кривых Безье не нужно указывать соотношение наклона и длину проекции, то через кривые можно выводить прямые отрезки и векторы под любым углом.
Так же была проблема с определением области рисунка. В LaTeX область рисования указывается вручную, и пользователю, как и примитивы, тоже приходится подбирать приблизительно, определяя, каких размеров будет рисунок. Благодаря автоматической обрезке PaintTeX определяет границы прямоугольника (холста), в котором было нарисовано изображение и обрезает рисунок до нужных размеров, вставляя соответствующие параметры в команду begin{picture}().
Другая проблема - работа с координатами Windows и LaTeX. Поскольку начальной точкой координат в Windows является верхний левый край окна, а в LaTeX нижний левый, при преобразовании рисунка в файл сохранялись координаты Windows, а после компиляции изображение выглядело в зеркальном отображении по вертикали. Теперь PaintTeX при сохранении рисунка учитывает этот нюанс.
Литература