Применение динамических систем, использующих метод вероятностного клеточного автомата при имитационном моделировании процесса распространения эпидемии холеры

Скворцов Андрей Викторович,

кандидат технических наук, доцент,

Башабшех Мурад Махмуд,

аспирант.

Научный руководитель – профессор, доктор технических наук

Масленников Борис Иванович.

Тверской государственный технический университет.

Application of dynamic systems using probabilistic cellular automaton to simulation modeling the spread of cholera

M.M.Bashabsheh,

Postgraduate,

A.V.Skvortsov,

Ph.D., docent,

B.I.Maslinkov,

Scientific director – Dr. Sc., Professor.

Tver State Technical University «TSTU», Tver.

The article considers the combination of spatial distribution models for cholera epidemic diseases using probabilistic cellular automaton. Epidemic is spatially distributed dynamic system to describe the space-time behavior of a class of models is possible to use cellular automata. Cellular automata (CA) are discrete dynamical systems, a collection of identical cells in the same way connected to each other. In cellular automata as models of computation are not considered input and output actions [1].

In the construction of the combined models is carried out preliminary decomposition process of the functioning of the object. Compartments may be real biological or social facilities, and may be simply a convenient mathematical abstraction. In this community, where the epidemic proceeds divided into several groups (compartments) based on property values ​​that are important from an epidemiological point of view [2].

Figure 1 shows the distribution model for cholera epidemic disease. Mathematical analysis of the model of the transmission dynamics of cholera, which describe three groups: susceptible to the disease (Susceptible), infected, infected susceptible (Infectious) and recovered receiving long-term immunity (Recovered), and two states for V. Cholera: Highly infectious cholera vibrios , Low-infectious cholera vibrios . The total population, N, is constant as well as having α, constant birth and death rate, µ. Infection is caused by ingesting contaminated water with either  hyper infective (HI vibrios/ml), or  lower infective (non-HI vibrios/ml) with the rate  and , respectively. It is also assumed, when  = и  =, the probability of ingestion resulting disease is 0.5. ξ is the rate at which I class contributes to HI and  is the rate at which HI progress to . Moreover, γ is the rate at which cases are recovered, while  is the rate where the vibrio cholera loses its viability in the aquatic environment [3].

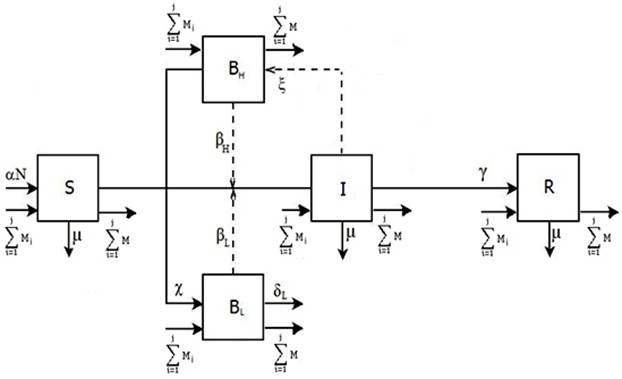
Fig. 1. Compartment models of the epidemic of cholera, S - number of the susceptible, I - number of the infected, R - number of the recovered,  - hyper infectious V. cholera,  - lower infective, a - natural human birth,  - rate of drinking contaminated HI V. cholera water,  - rate of drinking contaminated LI V. cholera water,  - HI v.cholerae infectious concentration,  - non-HI v.cholerae infectious concentration, ξ - rate of contribution to HI v.cholerae in aquatic environment, χ - rate of decay of HI to LI V. cholera , g - rate of recovery from cholera,  - death rate of non-HI vibrio in the environment, m - death rate, N - the total population, M - coefficient of the rate of migration, j - number of neighbors.

Fig.1. given by a system (1) of differential equations of the model are given control of cholera for the stochastic epidemic model (at Δt = 1) [3]:

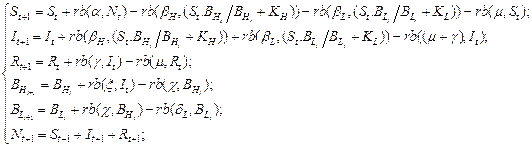 (1)

- number of susceptible individuals in population at time t, - number of infected individuals in population at time t, - number of recovered individuals in population at time t,- number of hyper infective at time t,- number of lower infective at time t, rb- random variate from a binomial distribution. If rb= Randbinom (p;n), then р- probability of success in a single trial, n- number of trials [3].

Selection of individuals for migration can occur as follows: The intensity of migration is constant for the entire population. Migration occurs in all groups evenly.

The essence of the method of modeling the spatial spread of epidemic diseases is to use a combination of mathematical models. The proposed model is a probabilistic cellular automaton, each element of which is a model of the unit with a global population mixing. Dynamics of the cell is described by a stochastic model for the spread of disease considering migration [4].

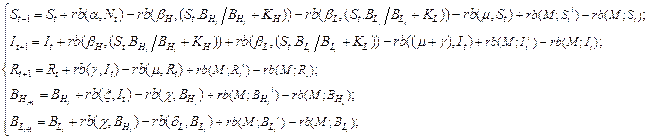To solve the system (1) are the recurrence relations (2), the combination of spatial distribution models for cholera epidemic diseases using probabilistic cellular automaton (Δt = 1) of the form [3, 4]:

Conclusion

Thus, in the combined model of the epidemic of cholera, using cellular automata found that the migration flows that cause mixing in the population, leading to activation of the epidemic process in initially "healthy" elementary populations and spatial transfer of the epidemic.

Migration rates have a significant effect on the transmission and distribution of infection in each cell. As a result, the cells acquire characteristics from each other, under the influence of the migration rate.

References

1.                В.К. Ванаг Исследование пространственно распределенных динамических систем методами вероятностного клеточного автомата (рус.) // Успехи физических наук. Обзоры актуальных проблем. : журнал. — май 1999. — Т. 169. — № 5. — С. 481-505.

2.                Масленников. Б. И. Математическое обеспечение информационно-аналитической медицинской системы программные продукты и системы/ Б. И. Масленников, А. В. Скворцов международное научно-практическое приложение к международному журналу «Проблемы теории и практики управления».- 2008.- C. 158-160.

3.                David M. Hartley, J. Glenn Morris Jr., and David L. Smith. Hyper infectivity: A Critical Element in the Ability of V. Cholerae to Cause Epidemics.

4.                Каток. А. Б. Перемешивание (динамические системы), введение в современную теорию динамических систем / А. Б. Каток, Б. Хасселблат.

Поступила в редакцию 05.04.2013 г.