Вейвлет-сжатие сигналов ультразвукового контроля
Чурова Валентина Владимировна,
аспирант кафедры «Методы и приборы неразрушающего контроля»,
Лезевская Анастасия Эдуардовна,
Титов Александр Игоревич,
Большакова Валерия Валерьевна,
студенты кафедры «Методы и приборы неразрушающего контроля».
Научный руководитель – кандидат технических наук, доцент кафедры «Методы и приборы неразрушающего контроля»
Кособоков Дмитрий Вячеславович.
Петербургский государственный университет путей сообщения.
Введение
Высокие требования к безопасности сложных технических объектов обуславливают необходимость проведения неразрушающего контроля (НК) изделий на стадии производства и эксплуатации. Применение автоматизированных средств НК с многоканальными схемами прозвучивания повышает качество выпускаемой продукции металлообработки. При этом увеличивается количество информации, получаемое в результате ультразвукового контроля (УЗК), что в свою очередь ведет к увеличению требуемых объемов памяти для хранения. Для внедрения паспортизации объекта контроля также необходимо иметь возможность восстановления информации обо всех сигналах, полученных в процессе дефектоскопирования.
Очевидным способом решения проблемы рационального уменьшения объема данных без искажения результатов контроля является применение алгоритма сжатия сигналов, что позволит в несколько раз сократить требования к объему устройств хранения и пропускной способности каналов связи. Существующие универсальные алгоритмы сжатия не учитывают специфику ультразвуковых (УЗ) сигналов, что не позволяет получить существенного (более чем в 2-3 раза) уменьшения объема данных. Таким образом, задача разработки специализированного алгоритма для сжатия данных УЗК является актуальной.
В настоящее время для сжатия и фильтрации сигналов широко применяется вейвлет-преобразования (ВП) [11,13]. Частотно-временная локализация вейвлетов позволяет анализировать свойства сигнала на разных частотах в разных точках исследуемого интервала, а также точно представлять сложные нестационарные сигналы с помощью различных базисных функций. Свойства вейвлетов делают целесообразным их использование для обработки сигналов УЗК, так как УЗ сигналы являются нестационарными, а эхо-сигналы от дефектов представляют собой локальные изменения амплитуды.
Обзор применения вейвлетов для обработки сигналов УЗК [2,4,7,8,9,10] показал, что ВП применяется, в основном, для улучшения выявляемости дефектов за счет повышения отношения сигнал/шум [2, 7, 8, 9, 10]. Известна также работа [4] по сжатию сигналов на основе ВП. Во всех рассмотренных работах для обработки сигналов УЗК используются известные в литературе приемы: пороговая обработка детализирующих коэффициентов, одномерное ВП разверток типа «А»[1] и двумерное ВП разверток типа «В», «С» и «D»[2]. Наиболее распространенные базисы ВП – вейвлеты Добеши и симлеты.
1. Разработка алгоритма сжатия
Известный в
литературе [1, 11, 13] метод сжатия сигналов и изображений с использованием
вейвлетов основан на разбивке сигнала на две составляющие – низкочастотную (НЧ),
или аппроксимирующую, ![]() и высокочастотную (ВЧ), или детализирующую,
и высокочастотную (ВЧ), или детализирующую,
![]() . После вейвлет-разложения
детализирующие коэффициенты модифицируются – округляются, подвергаются
пороговой обработке с различными правилами выбора порога (адаптивный порог,
эвристический, минимаксный и т.д.) или полностью отбрасываются.
. После вейвлет-разложения
детализирующие коэффициенты модифицируются – округляются, подвергаются
пороговой обработке с различными правилами выбора порога (адаптивный порог,
эвристический, минимаксный и т.д.) или полностью отбрасываются.
Задачи НК
требуют сохранения как можно более полной информации о дефектах и возможности
полной и точной реконструкции полезного сигнала, поэтому при выборе базиса ВП будем
руководствоваться следующими требованиями к вейвлетным функциям:
ортогональность, симметрия, компактный носитель, близость к форме УЗ
эхо-сигнала. Проблему выбора базисных функций позволяет решить применение
биортогонального ВП, для которого действительны все свойства ортогонального:
существование ![]() и возможность реализации
быстрого ВП. Большое число нулевых моментов дает хорошие результаты при сжатии
информации, а степень гладкости вейвлета обеспечивает точную реконструкцию
сигналов. При использовании биортогональной пары декомпозиция сигналов может
производиться вейвлетом
и возможность реализации
быстрого ВП. Большое число нулевых моментов дает хорошие результаты при сжатии
информации, а степень гладкости вейвлета обеспечивает точную реконструкцию
сигналов. При использовании биортогональной пары декомпозиция сигналов может
производиться вейвлетом ![]() , а реконструкция
парным вейвлетом
, а реконструкция
парным вейвлетом ![]() , или наоборот. При этом оба
вейвлета можно выполнить симметричными.
, или наоборот. При этом оба
вейвлета можно выполнить симметричными.
Особенностью данной работы также является то, что сжатие сигналов УЗК будет проводиться не по направлению распространения сигнала, а по направлению сканирования, что даст хорошие результаты при сжатии результатов контроля протяженных объектов.
Разработанный алгоритм сжатия сигналов УЗ контроля на основе ВП состоит из следующих основных этапов:
1. Вейвлет-разложение сигнала.
2. Модификация коэффициентов разложения.
3. Поиск областей ненулевых коэффициентов.
4. Сохранение результатов сжатия.
На этапе 1
выполняется одноуровневое разложение сигнала ![]() на
сумму аппроксимирующих и детализирующих составляющих:
на
сумму аппроксимирующих и детализирующих составляющих:
![]() (1)
(1)
где ![]() ,
, ![]() и
и ![]() – функции дискретной переменной
– функции дискретной переменной ![]() ,
,
n = 0,
1, 2,…, M-1; ![]() – аппроксимирующие коэффициенты;
– аппроксимирующие коэффициенты; ![]() – детализирующие коэффициенты; j
– параметр масштаба; k – параметр сдвига.
– детализирующие коэффициенты; j
– параметр масштаба; k – параметр сдвига.
Применяется частотный подход к ВП, согласно которому кратномасштабный анализ сигнала рассматривается как поэтапная процедура фильтрации [13].
На этапе 2 коэффициенты разложения подвергаются модификации. Прежде всего, отбрасываются детализирующие коэффициенты. Причина такого подхода заключена в предположении, что НЧ область содержит больше информации об исходном сигнале, а ВЧ область – больше информации о помехах. Аппроксимирующие коэффициенты проходят пороговую обработку и округляются до целого значения.
На этапе 3 по каждой строке матрицы аппроксимирующих коэффициентов производится поиск областей коэффициентов, отличных от нуля. Информация о найденных областях сохраняется на этапе 4 в специальном формате: координата начала области; протяженность области; значения коэффициентов внутри области.
Алгоритм восстановления сигнала по сжатым данным включает в себя процедуры: считывание сжатых данных; восстановление матрицы коэффициентов; обратное ВП.
2. Экспериментальное исследование алгоритма сжатия
Экспериментальное исследование алгоритма сжатия было выполнено в два этапа: на первом этапе использовались модельные данные, на втором этапе – реальные данные, полученные в результате УЗ контроля металлопроката.
Для проведения исследования на первом этапе были смоделированы сигналы УЗ контроля сварного шва трубопровода (сталь) эхо-импульсным методом при озвучивании наклонным совмещенным пьезоэлектрическим преобразователем (ПЭП) с круглым пьезоэлементом. В качестве модели дефекта была выбрана сфера радиусом 2 мм, расположенная в центральном продольном сечении сварного шва. Для расчета амплитуд эхо-сигналов использованы приближенные формулы акустического тракта с учетом диаграмм направленности излучателей в основной и дополнительной плоскости [3, 5, 6]. Для моделирования случайных помех, возникающих в электроакустическом тракте, на огибающую эхо-сигналов накладывалась помеха в виде случайного шума, уровень которого задавался в процентах от максимальной амплитуды эхо-сигнала от модели дефекта. Сигналы отображены на D-развертке (вид представления информации, при котором принимаемые сигналы отображаются в некотором масштабе в виде точек на продольном сечении объекта контроля (ОК), перпендикулярном поверхности сканирования и перпендикулярном направлению прозвучивания (акустической оси звукового пучка). Кроме сигналов с различным уровнем шума была смоделирована D-развертка с уровнем шума 0%, которая принята в качестве эталонной.
На рис.1а приведено изображение D-развертки с уровнем случайного шума 30%, а на рис.1б – аппроксимирующие и детализирующие коэффициенты ВП. Видно, что практически вся информация о дефекте содержится в низкочастотной компоненте, а высокочастотная компонента содержит только шумовую составляющую.
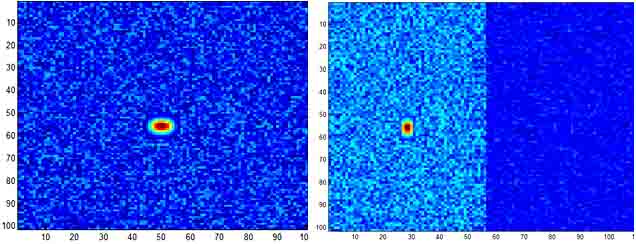
Координата ПЭП, дискреты
а) б)
Рис. 1. Отображение смоделированного эхо-сигнала на D-развертке: а) исходный сигнал; б) коэффициенты вейвлет-разложения.
На смоделированных D-развертках проведено экспериментальное исследование 3-х алгоритмов:
1. Алгоритм 1 – разработанный алгоритм сжатия сигналов УЗ контроля. Результаты сжатия сохраняются в специальном формате.
2. Алгоритм 2 – пороговая обработка амплитуд эхо-сигналов. Результаты сохраняются в формате исходных данных.
3. Алгоритм 3 – пороговая обработка амплитуд эхо-сигналов с последующим ВП. Аппроксимирующие коэффициенты округляются и сохраняются в специальном формате.
4. Алгоритм 4 – применение универсального алгоритма сжатия без потерь.
В ходе исследования алгоритмов для смоделированных D-разверток с уровнем случайного шума 5, 10, 20, 30, 40 и 50% рассчитаны фактор сжатия Fсж [12]:
![]() (2)
(2)
и пиковое отношение уровня сигнала к шуму PSNR (peak signal-to-noise ratio) [14]:
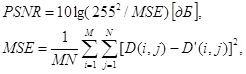 (3)
(3)
где MSE (mean square error) - среднеквадратичная ошибка; M и N – количество строк и столбцов D-развертки; D (i, j) – элемент D-развертки, полученной в результате восстановления сжатых данных; D' (i, j) – элемент «эталонной» D-развертки без добавления случайного шума.
В алгоритмах 1 и 3 производилось одноуровневое одномерное вейвлет-разложение по каждой строке D-развертки, в качестве базисных функций вейвлет-разложения выбраны биортогональные вейвлеты bior2.6. Перед расчетом Fсж исходные сигналы и результаты сжатия по алгоритмам 1-3 дополнительно обрабатывались одним из существующих универсальных алгоритмов сжатия данных без потерь. Устанавливаемые пороговые значения обработки аппроксимирующих коэффициентов или амплитуд исходного сигнала изменялись от 0 до максимального значения коэффициентов или амплитуд сигнала. В каждом отдельном опыте устанавливалось пороговое значение th = n·Δth , где n – номер опыта; Δth - шаг изменения порога.
Полученные зависимости PSNR и Fсж от n для всех алгоритмов и уровней шума имеют характерный вид (рис.2), который объясняется следующим: при увеличении порогового значения из зашумленного сигнала удаляется все больше помех, восстановленный сигнал приближается к эталонному и, следовательно, PSNR увеличивается. Точка максимума PSNR (точка Е на рис.2) соответствует опыту, в котором полностью удаляется шумовая составляющая сигнала, что является наилучшим результатом. При дальнейшем увеличении порога начинает искажаться эхо-сигнал от дефекта и PSNR уменьшается до некоторого значения, соответствующего полному исчезновению сигнала.
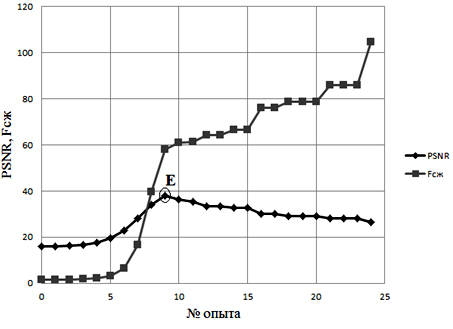
Рис. 2. График PSNR и фактора сжатия для алгоритма 1 и D-развертки с уровнем шума 30%.
Результаты расчета Fсж и PSNR после сжатия алгоритмами 1, 2, 3 сигналов с различным уровнем шума представлены в табл.1 и на рис.3а,б. Все данные приведены для точки E (точки максимума PSNR), определение которой поясняет рис.2. Для сравнения в табл.1 и на рис.3а приведены результаты обработки исходных сигналов по алгоритму 4.
Таблица 1.
Результаты расчета фактора сжатия и PSNR.
|
Уровень шума, % |
Алгоритм 1 |
Алгоритм 2 |
Алгоритм 3 |
Алгоритм 4 |
|||
|
Fсж |
PSNR |
Fсж |
PSNR |
Fсж |
PSNR |
Fсж |
|
|
5 |
25 |
49 |
21 |
55 |
22 |
52 |
3,4 |
|
10 |
33 |
46 |
27 |
47 |
29 |
47 |
2,8 |
|
20 |
54 |
39 |
41 |
40 |
44 |
41 |
2,1 |
|
30 |
58 |
38 |
49 |
37 |
53 |
38 |
1,9 |
|
40 |
63 |
35 |
54 |
35 |
60 |
35 |
1,8 |
|
50 |
70 |
33 |
61 |
33 |
60 |
33 |
1,7 |
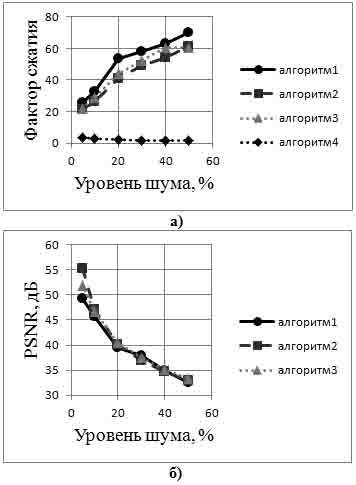
Рис. 3. Графики фактора сжатия и PSNR.
Результаты экспериментального исследования на модельных данных показали, что самым эффективным с точки зрения сжатия сигналов алгоритмом является алгоритм 1. Значение фактора сжатия при обработке по этому алгоритму на 15-31% (в зависимости от уровня шума) больше, чем при использовании алгоритма 2, и на 4-22% больше, чем при использовании алгоритма 3 (табл. 1). Таким образом, разработанный алгоритм позволяет производить более эффективное сжатие по сравнению с обычной пороговой обработкой амплитуд сигналов. Фактор сжатия зависит также от уровня шума на дефектограмме. Чем выше интенсивность помехи, тем лучшее сжатие сигнала можно получить за счет удаления шумовой составляющей при применении специализированных алгоритмов сжатия на основе ВП и пороговой обработки. Универсальные алгоритмы не дают преимущества при сжатии случайных данных: не позволяют получить сжатие более чем в 3 раза и имеют практически постоянное значение фактора сжатия для сигналов с различным уровнем помех, что видно из таблицы 1 и рисунка 3 (а).
Результаты исследования также позволили дать рекомендации по выбору порогового уровня обработки коэффициентов ВП: порог должен выбираться в соответствии с уровнем присутствующего на дефектограмме шума, требуемым фактором сжатия и ошибкой восстановления, но в любом случае не должен превышать значение, соответствующее точке максимума PSNR, рассчитанного по выражению (3). Дальнейшее увеличение порога неэффективно, так как сжатие при этом происходит за счет потери полезной информации, а также наблюдается уменьшение PSNR при небольшом увеличении фактора сжатия (рис. 2).
Стоит отметить, что все результаты получены на модельных данных. Для реальных данных, получаемых в процессе УЗ контроля, следует ожидать других значений фактора сжатия, а также качества фильтрации и восстановления. Алгоритм сжатия должен адаптироваться к конкретному виду УЗ сигналов и помех. Особенности и полученные результаты применения предложенного алгоритма сжатия на реальных данных будут рассмотрены в следующей статье.
4. Основные результаты и выводы
1. Разработан алгоритм сжатия сигналов УЗ контроля, состоящий из следующих операций: вейвлет-разложение сигнала; удаление детализирующих коэффициентов и пороговая обработка аппроксимирующих коэффициентов ВП; поиск коэффициентов, отличных от нуля и объединение их в области; сохранение выделенных областей в специальном формате.
2. Проведено экспериментальное исследование разработанного алгоритма на модельных данных. На основании расчета фактора сжатия показано, что данный алгоритм обеспечивает лучшее сжатие дефектограмм с различным уровнем шума по сравнению с пороговой обработкой амплитуд исходного сигнала, а также по сравнению с универсальными алгоритмами сжатия данных.
3. Для D-разверток с уровнем случайного шума 5, 10, 20, 30, 40 и 50% от максимальной амплитуды эхо-сигнала предельные значения фактора сжатия в точке максимума PSNR составили диапазон 25÷70 бит/бит. Значения PSNR при этом вошли в диапазон типичных значений PSNR для сжатия изображений с потерями (30÷50 дБ) и составили 33÷49 дБ.
Работа выполнена при поддержке Петербургского государственного университета путей сообщения инициативных научных работ, выполняемых студенческими научными коллективами.
Литература
1. Гонсалес Р., Вудс Р. Цифровая обработка изображений. – М.: Техносфера, 2005. – 1072 с.
2. Гуань Янь, Ки Жень, Пейвен Ке. Адаптивная вейвлет-пакетная декомпозиция, основанная на алгоритме согласованного преследования и ее применение в ультразвуковом контроле. – Дефектоскопия, 2007, №1, с.80-87.
3. Гурвич А.К., Ермолов И.Н. Ультразвуковой контроль сварных швов. Киев: Техника, 1972.
4. Ки Жень, Тяньлу Чен, Пейвен Ку, Яшень Синь. Сжатие ультразвуковых сигналов по лифтинговой схеме вейвлетного преобразования. – Дефектоскопия, 2008, №7, с.68-73.
5. Кретов Е.Ф. Ультразвуковая дефектоскопия в машиностроении. – Спб: Изд-во «СВЕН», 2007. 296 с.
6. Методы акустического контроля металлов / Н.П. Алешин, В.Е Белый, А.Х. Вопилкин, А.К. Вощанов, И.Н. Ермолов, А.К. Гурвич: Под ред. Н.П. Алешина. – М.: Машиностроение, 1989. – 456 с.
7. Перов Д.В., Ринкевич А.Б., Смородинский Я.Г. Вейвлетная фильтрация сигналов ультразвукового дефектоскопа. – Дефектоскопия, 2002, №12, с.3-20.
8. Перов Д.В., Ринкевич А.Б. Вейвлетный анализ акустических полей и сигналов в ультразвуковой дефектоскопии. – Дефектоскопия, 2005, №2, с.43-54.
9. Перов Д.В., Ринкевич А.Б., Смородинский Я.Г. Применение вейвлетов для анализа ультразвуковых полей, детектированных лазерным интерферометром. Обнаружение и локализация дефекта в монокристалле алюминия. – Дефектоскопия, 2001, №12, с.67-79.
10. Перов Д.В., Ринкевич А.Б. Фильтрация ультразвуковых сигналов лазерного интерферометра с использованием диадного вейвлет-преобразования. – Дефектоскопия, 2002, №4, с.78-98.
11. Смоленцев Н.К. Основы теории вейвлетов. Вейвлеты в MATLAB. – М.: ДМК Пресс, 2005. – 304 с.
12. Сэломон Д. Сжатие данных, изображений и звука. М.: Техносфера, 2004. - 368с.
13. Яковлев А.Н. Введение в вейвлет-преобразования: Учеб. пособие. – Новосибирск: Изд-во НГТУ, 2003. – 104 с.
14. Alain Horé, Djemel Ziou. Image quality metrics: PSNR vs. SSIM. – International Conference on Pattern Recognition, IEEE Computer Society Press, 2010.
Поступила в редакцию 01.03.2013 г.
[1] Развертка типа «А» - одномерная функция, описывающая зависимость амплитуды сигнала от времени распространения УЗ колебания
[2] Развертки типа «В», «С», «D» - двумерные функции, представляющие собой проекции изображения внутренней структуры объекта контроля на ту или иную плоскость.