Моделирование элементов конструкции микромеханического акселерометра

Первадчук Владимир Павлович,

доктор технических наук,

Шадт Артём Константинович,

аспирант.

Пермский национальный исследовательский политехнический университет.

Микромеханические акселерометры широко применяются в космических аппаратах, авиации, автомобилестроении, высокоточном оружии – управляемых ракетных и артиллерийских снарядах [2, 4]. Акселерометры с малым диапазоном измерения используются для измерений углов наклона приборов, выходной сигнал акселерометра пропорционален синусу угла наклона по отношению к горизонту [3]. Один из важнейших элементов конструкции микромеханических акселерометров – подвесы (торсионы), их форма и размеры определяют важный параметр микроприборов – чувствительность.

При разработке акселерометра маятникового типа имеется возможность вариации геометрии чувствительного элемента и упругих подвесов. Для изготовления чувствительного элемента (ЧЭ) и торсионов используется монокристаллический кремний, например марки КЭФ-4,5 (100), обладающий необходимыми механическими свойствами [1]. Проведен расчет влияния технологических отклонений при изготовлении маятника на максимальное напряжение в упругих подвесах.

Анализ упругих подвесов различной конфигурации проводился методом компьютерного моделирования в среде ANSYS , которая представляет собой набор программных пакетов, предназначенных для решения обширного класса задач методом конечных элементов [4]. Проведен расчет статического напряженно-деформированного состояния подвесов различной конфигурации при приложении момента сил, соответствующего моменту инерционной массы чувствительного элемента акселерометра, а также моделирование и анализ форм колебаний и собственных частот колебаний чувствительного элемента с подвесами, имеющими различную форму сечения.

В расчетах были использованы конструкции чувствительного элемента компенсационного акселерометра выпускаемого серийно, с формой упругого подвеса изображенной на рис. 1, а также конструкция опытного образца на базе серийного акселерометра с крестообразной формой упругого подвеса (рис. 2).

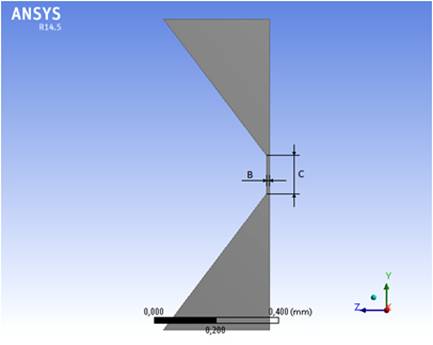
Рис. 1. Сечение упругого подвеса серийно выпускаемого акселерометра.

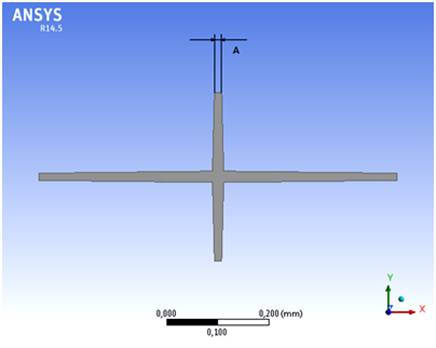
Рис. 2. Сечение упругого подвеса крестообразного сечения.

Конструкция чувствительного элемента (ЧЭ) для компенсационного акселерометра представлена на рис. 3. ЧЭ представляет собой симметричный маятник, с ассиметрично расположенной инерционной массой, подвешенный на двух упругих балках (торсионах) к неподвижной центральной части. Принцип действия ЧЭ основан на несимметричном подвесе инерционной массы, благодаря чему осуществляется регистрация ускорения, направленного перпендикулярно плоскости ЧЭ. Для создания необходимой величины зазора между чувствительным элементом и расположенной под ним платой центральная часть ЧЭ имеет выступающие платики с каждой стороны (рис. 3б). Поверхности основания и подвижной части ЧЭ находятся в одной плоскости.

Проведен расчет влияния технологических отклонений толщины упругого подвеса в пределах поля допуска для ЧЭ серийного акселерометра и опытного образца с крестообразным упругим подвесом. К подвижной части ЧЭ прикладывался момент сил 10^-4 Н∙мм. Приложенный момент сил вызывает поворот подвижной части ЧЭ на определенный угол.

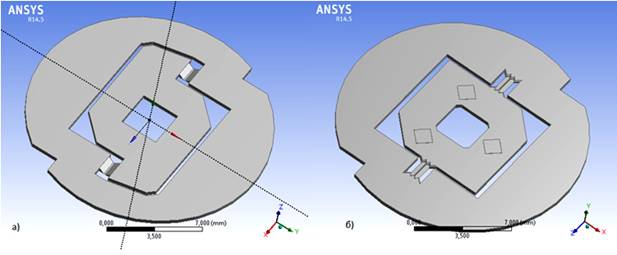
Рис. 3. а) маятник серийного акселерометра; б)маятник опытного образца.

Варьируя размеры упругого подвеса для обоих образцов ЧЭ были получены значения максимальных напряжений в торсионах. Для подвеса серийного акселерометра изменялась толщина и длина тонкой части подвеса (размеры В и С соответственно на рис. 1). На крестообразном подвесе изменялась ширина ребер с сохранением постоянного угла наклона граней ребер (размер А на рис. 2). Результаты приведены в табл. 1 и 2.

Таблица 1.

Результаты расчета влияния технологических отклонений в геометрических размерах крестообразного подвеса.

Таблица 2.

Результаты расчета влияния технологических отклонений в геометрических размерах подвеса серийного акселерометра.

Из таблиц видно, что при большем разбросе геометрических размеров крестообразного подвеса в пределах технологических допусков, изменение максимального напряжения при повороте на заданный угол незначительно отличается от изменений в подвесе изображенном на рис.1.

Также были рассчитаны значения собственных частот колебаний ЧЭ с упругими подвесами различных форм.

Таблица 3.

Результаты расчета собственных частот колебаний ЧЭ.

Для обеих разновидностей подвеса первая мода является рабочей, остальные паразитные. По результатам расчетов видно что в маятнике с крестообразным подвесом рабочая частота намного меньше паразитных по сравнению с подвесом изображенным на рис. 1. Это означает что крестообразный подвес имеет большую жесткость по паразитным степеням свободы в отличие от обычного подвеса.

Из вышеописанных результатов можно сделать вывод, что ЧЭ с крестообразным подвесом является более предпочтительным в виду меньшей чувствительности к отклонениям от заданных размеров подвесах, а также хорошей помехоустойчивости из-за большей жесткости по паразитным степеням свободы маятника. Результаты расчетов применяются при изготовлении опытных приборов с ЧЭ имеющим крестообразные упругие подвесы.

Литература

1.                  Бритков О.М. Разработка конструкции микромеханического акселерометра / 12 Всероссийская межвузовская научно-техническая конференция студентов и аспирантов «Микроэлектроника и информатика – 2005». – М.: МИЭТ, 2005, с. 123.

2.                  Мокров Е.А. Интегральные датчики. Состояние разработок и производства. Направления развития, объемы рынка. – Датчики и системы, 2000, № 1, с. 28–30.

3.                  Пешехонов В.Г. Ключевые задачи современной автономной навигации. – Гироскопия и навигация, 1996, № 1, с. 48–55.

4.                  Распопов В.Я. Микромеханические приборы. – Тула: Тульский госуниверситет, 2002, с. 795.

5.                  www.ansys.com.

Поступила в редакцию 11.09.2013 г.