Стабилизация кластерной экономики при наличии инвестиционных ресурсов
Сейдахметова Дана Уласбековна,
магистрант механико-математических факультета Казахского национального университета им. аль-Фараби.
В современной экономике, особенно в условиях глобализации, традиционное деление экономики на сектора или отрасли утрачивает мобильность. На первое место выходят кластеры – системы взаимосвязей фирм и организаций, значимость которых как целого превышает простую сумму составных частей. Кластерная политика оказывает влияние не только на функционирование самих организаций, но и на тот регион, где развивается кластер. Согласно М.Портеру, кластеры – это группа географически соседствующих взаимосвязанных компаний (поставщики) и связанных с ними организаций, действующих в определенных сферах и взаимодополняющих друг друга [2].
Одной из ключевых моделей экономического роста является модель трехсекторной экономики, которая состоит из:
1) материального сектора – предметы труда (топливо, электроэнергия, сырье и другие материалы);
2) фондосоздающего сектора – средства труда (машины, оборудование, производственные здания, сооружения и т.д.);
3) потребительского сектора – предметы потребления.
Анализ трехсекторной модели роста позволяет построить различные сценарии развития экономики, оценить последствия глобализации для энергетического сектора в условиях различных вариантов экономической политики, проводимой правительством.
Центральное место в трехсекторной экономике занимает фондосоздающий сектор. Именно его рост обеспечивает развитие материального и потребительского секторов.
Анализ трехсекторной модели роста позволяет построить различные сценарии развития экономики, оценить последствия глобализации для энергетического сектора в условиях различных вариантов экономической политики, проводимой правительством.
В соответствии с [1] рассмотрим трехсекторную модель отрасли в абсолютных показателях, которая включает:
1) четыре линейных динамических элемента первого порядка:
(1)
2) три линейных распределительных элемента:
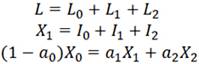(2)
3) три нелинейных статических элемента:
(3)
Ki – основные производственные фонды (ОПФ) секторов; L – общее число работников, занятых в производственной сфере; ν – темп прироста числа занятых работников; Li – число работников, занятых в i-м секторе; Xi – выпуск продукции в i-м секторе; Ii – инвестиции в i-й сектор; Fi – производственные функции в i-м секторе; ai – прямые материальные затраты на единицу продукции i-го сектора; μi – коэффициент износа ОПФ.
Постановка задачи. Оценить структурную устойчивость неподвижных точек для каждой области параметров (θi,si), обеспечивающих экономический рост фондовооруженности секторов.
Определение области параметров (θi,si) для обеспечения экономического роста. Пусть использованы производственные функции (3) Кобба — Дугласа
(4)
где Ai – коэффициент нейтрального технического прогресса; αi – коэффициент эластичности по фондам.
Обозначим через θi=Li/L, si=Ii/X1 (i=0,1,2) доли секторов в распределении трудовых и инвестиционных ресурсов (2), удовлетворяющих условиям сбалансированности
(5)
Тогда уравнение материального баланса принимает вид
(6)
а производственные функции (4) определяются в относительных показателях:
(7)
где xi=Xi/L, ki=Ki/Li (i=0,1,2) — производительность труда и фондовооруженность в расчете на одного занятого в i-м секторе соответственно.
Используя описанные выше уравнения, можно выявить технологически возможные сбалансированные стационарные состояния трехсекторной экономики на всем диапазоне изменения параметров распределения трудовых и инвестиционных ресурсов. Ниже рассматривается задача с фиксированным распределением инвестиционных ресурсов.
Эти состояния определяются с целевой функцией и двумя уравнениями трудового и материального балансов:
(8)
где
,
Используя
условие 
определим
доли фондосоздающего и потребительскогосекторов в распределении трудовых
ресурсов в следующем виде, при 0 ≤ z ≤ 1:
Огранияение запишем в следующем виде:
Отсюда находим
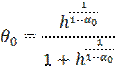
Подставив полученную зависимость в функцию цели, решим задачу, находим значение z*, из условия
max f(z) = f(z*)
Тогда имеем
, 
, 
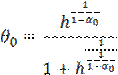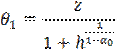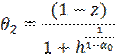
и 
, 
, 
Решим эту задачу со следующими параметрами:
Из
таблицы 1 и графиков на рисунке 1 видно, что при движении по траектории в распределении
ресурсов функция f(z) достигает максимального значения 8,908 при z*=0,4, следовательно
h*=0,48. Теперь определим значения 
:
θ0 = 0,21 , θ1 = 0,355 , θ2 = 0,434.
Зная h, определяем удельные выпуски секторов: x0 = 39, x1 = 21.8, x2 = 17.2.
Таблица 1.
Доли секторов в ресурсах.
|
z |
0 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1 |
|
h |
0 |
0,36 |
0,41 |
0,45 |
0,48 |
0,50 |
0,51 |
0,52 |
0,53 |
0,52 |
0,47 |
|
f(z) |
0 |
6,05 |
7,71 |
8,55 |
8,908 |
8,906 |
8,58 |
7,93 |
6,86 |
5,13 |
0 |
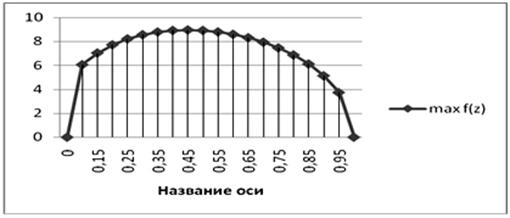
Рис. 1. изменение долей материального, фондосоздающего и потребительского секторов.
Из проведенного теоретического исследования состояний трехсекторной экономики видно, что продвижение к точке глобального максимума сопровождается все большими расходами средств производства на каждую новую единицу выпуска предметов потребления. Эту точку необходимо знать для того, чтобы суметь определить направление наиболее целесообразного движения в пространстве свободных переменных.
Литература
1. Колемаев В.А. «Экономико-математическое моделирование. Моделирование макроэкономических процессов и систем: учебник для студентов вузов». – М.: ЮНИТИ-ДАНА, 2005.-295 с.
2. Портер Э.М. «Конкуренция»: Пер.с англ. – М.:Издательский дом «Вильямс», 2005 – 608 с.: ил. – Парал. тит. англ.
Поступила в редакцию 06.02.2013 г.