Функция кратности непрерывного спектра дифференциального оператора второго порядка

Филиппенко Виктор Игнатьевич,

кандидат физико-математических наук, доцент кафедры математики Института сервисного обслуживания и предпринимательства (филиала ДГТУ).

Пусть - гильбертово пространство векторов  с евклидовым скалярным произведением  и нормой . Если векторы  и  рассматривать как матрицы-столбцы, то .

Обозначим через  гильбертово пространство всех - мерных вектор-функций, значения которых принадлежат , а квадрат нормы суммируем, т. е. 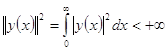. Скалярное произведение в пространстве  определяется следующим образом: .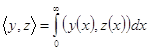

Пусть , где - вещественная матричная функция порядка , которая измерима и локально суммируемая в сильном смысле. При каждом . Предположим, что  имеет смысл для каждой функции , которая на любом отрезке  абсолютно непрерывна вместе со своей первой производной, а . Предполагается, что уравнение  имеет ровно  решений, принадлежащих . Такая ситуация имеет место, например, если  удовлетворяет условиям  при любом векторе  из пространства , а функция непрерывная, монотонная и .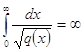

В этой статье определяется поведение функции кратности непрерывного спектра самосопряженного дифференциального оператора, порожденного формально самосопряженным дифференциальным выражением  в гильбертовом пространстве .

Пусть  - замкнутый симметрический оператор с минимальной областью определения, порожденный в пространстве  операцией . Индекс дефекта оператора  предполагается равным . Стандартным образом можно построить формулу обобщенных резольвент  оператора , а затем описывается множество всех спектральных функций  оператора [1].

1. Пусть  и  решения матричного уравнения , удовлетворяющие начальным условиям , где  и  - единичная и нулевая матрицы порядка . Матричные функции  и  составляют фундаментальную систему решений и являются целыми функциями параметра . Известно, что если уравнение  имеет ровно  линейно независимых решений, принадлежащих , то в этом и только в этом случае существует единственная симметрическая матрица  такая, что все столбцы матрицы  принадлежат  и , где .

Каждой вектор-функции , для которой  имеет смысл, поставим в соответствие вектор-функцию , которую будем рассматривать как матрицу-столбец. Введем в рассмотрение ортогональную кососимметрическую порядка  матрицу

.

Для любых вектор-функций  и , к которым применима операция , тождество Лагранжа может быть записано в виде

,

где звездочкой отмечен переход к сопряженной матрице, в данном случае – однострочной.

Имеет место Лемма. В верхней полуплоскости комплексной плоскости  матричная функция  является регулярной, причем .

Доказательство строим по схеме, изложенной в [1]. Рассмотрим самосопряженное расширение  оператора , заданное краевым условием . Ортогональная резольвента оператора  определяется формулой . Следовательно,  является решением уравнения

,                                                                                                          (1)

которое принадлежит области определения  оператора . Применяя метод вариации произвольных постоянных, получим для любой финитной вектор-функции  из пространства  решение уравнения (1)

.

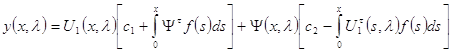Из условия  следует, что , а так как , то

.

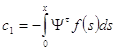Следовательно

,

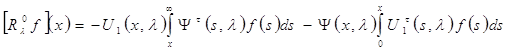или короче:

,

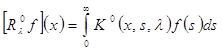где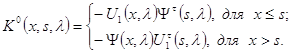

Для функции  имеет место соотношение .

Пусть  где  произвольный вектор из пространства . Согласно последним равенствам  при любом  и любом  является регулярной в верхней полуплоскости функцией параметра  с неотрицательной мнимой частью. В силу нормальности семейства таких функций и произвольности вектора  регулярной в верхней полуплоскости является и .

Последнее утверждение леммы следует из равенства .

2. Пусть  - самосопряженное расширение оператора  в пространстве , определяемое разделяющимися краевыми условиями. Эти условия в точке  можно представить в виде , где - некоторая прямоугольная матрица, состоящая из  линейно независимых строк и  столбцов, удовлетворяющих условию . Далее, применяя лемму, убеждаемся в справедливости следующей теоремы.

Теорема

Пусть для любого  уравнение  имеет линейно независимых решений  таких, что:

1) ;

2) , какова бы ни была функция ;

3) линейная комбинация  удовлетворяет системе краевых условий в точке  только в том случае, когда ;

4) вектор-функции  удовлетворяют условию Липшица на сегменте . Тогда ранг спектральной матрицы-функции оператора  на сегменте  не превосходит .

Воспользуемся стандартным определением функции кратности спектра.

Следствие

Если выполняются условия теоремы и , где  - постоянная эрмитова матрица с простыми собственными значениями, а - некоторая эрмитова матрица с суммируемыми на промежутке  элементами, то функция кратности непрерывного спектра  оператора - кусочно-постоянная, ее значение в точке  определяется числом собственных значений матрицы , удовлетворяющих условию .

Литература

1.                  Филиппенко В.И. Резольвенты линейного оператора, порожденного обобщенным квазидифференциальным выражением // В сб.: Исследования по комплексному анализу, теории операторов и математическому моделированию.- Владикавказ: Изд-во ВНЦ РАН, 2004. - С. 304 – 322.

Поступила в редакцию 30.08.2013 г.