Анализ подходов к разрешению противоречий в процедурах измерения и оценивания результатов критериально-ориентированного тестирования в современных компьютерных системах тестирования
Туктаров Ринат Равильевич,
старший преподаватель факультета военного обучения Государственного морского университета им. адмирала Ф. Ф. Ушакова.
Компьютерные системы тестирования (КСТ), как средства автоматизации функции оценки знаний обучающегося (этап усвоения знаний), на современном этапе, с учетом целей и задач критериально-ориентированного тестирования, должны отвечать определенным требованиям, относящимся к процедурам измерения и оценивания результатов тестирования в КСТ.
В целях контроля усвоения знаний в настоящее время используются большое число КСТ, как выполненных в виде отдельных программных продуктов (например, ITEMAN, RASCAL, RSP, The Examiner testing system, Fast TEST professional, C-Quest, CONTEST, SunRav TestOfficePro, HyperTest, UniTest System, TestMaster, AVELife TestGold Studio, АСТ-Тест Plus, ГРАММАТЕЙ-КЛАСС, ПОЛСТАР, «Контроль знаний», «Система проверки знаний», «Универсальный тестовый комплекс», «Экзаменатор», «Аттестация», УСАТИК и т.д.), так и встроенных в различные обучающие системы. Отсутствие стандарта или хотя бы общепринятых норм и правил создания таких систем привело к тому, что практически каждая из них является «вещью в себе» и не имеет описания алгоритмов функционирования, а в частности, ¾ описания реализуемых процедур оценивания результатов тестирования. При этом все они являются типичным представителем современных КСТ и не соответствуют своему предназначению по показателю критериальной валидности, т.е. не обеспечивают объективную оценку результатов тестирования в соответствии с мнением преподавателей.
Основными требованиями к процедурам измерения и оценивания результатов тестирования в КСТ являются:
1) объективность и дифференцированность первичных результатов тестирования;
2) формулировку оценки результатов тестирования в системе предпочтений преподавателя;
3) соответствие количественного выражения оценки объективному мнению преподавателя как эксперта в предметной области соответствующей учебной дисциплины и лица, принимающего решение (ЛПР) по управлению процессом обучения.
Анализ выполнения этих требований в современных КСТ выявляет наличие следующих противоречий:
1) противоречие между дифференцированностью результатов выполнения единичных тестовых заданий в формах «Множественный выбор», «Соответствие», «Упорядоченный список», «Открытый вопрос» и отсутствием объективных методов педагогического измерения результатов выполнения этих единичных заданий;
2) противоречие между требованиями квалиметрии и применением процедуры вывода интегрального показателя качества выполнения теста, которая некорректна в отношении имеемых способов представления результатов выполнения единичных тестовых заданий в формах «Множественный выбор», «Соответствие», «Упорядоченный список» и «Открытый вопрос»;
3) противоречие между достаточной дифференцированностью показателей качества и недостаточной дифференцированностью производных от них показателей уровня качества результатов критериально-ориентированного тестирования при их определении в современных КСТ;
4) противоречие между способностью КСТ адекватно воспроизводить имеемый метод задания системы предпочтений преподавателя и отсутствием метода адекватного представления этой системы предпочтений.
Таким образом, налицо существование тестологической проблемы измерения и оценивания результатов критериально-ориентированного тестирования, представленной совокупностью приведенных выше противоречий.
Наличие данной совокупности противоречий определяет актуальность разработки моделей и процедур педагогического измерения и критериально-ориентированного оценивания результатов контроля знаний в компьютерных системах тестирования как средств их разрешения.
Проведенный выше анализ существа выявленных противоречий позволяет утверждать, что средством разрешения первых двух из них является разработка метода оценки результатов выполнения единичных тестовых заданий в формах «Множественный выбор», «Соответствие», «Упорядоченный список», «Открытый вопрос». В литературе по педагогической тестологии имеется ряд указаний (Аванесов В.С., Свиридов А.П.), что перечисленные выше формы тестовых заданий с позиций процедур измерения и оценивания их результатов могут быть сведены к двум процедурам.
На основе результатов исследований В.С. Аванесова в диссертации И.П. Карповой показано, что формы единичных тестовых заданий «Множественный выбор» и «Открытый вопрос» на основе определенных моделей и процедур идентификации (распознавания) могут быть сведены к форме «Множественный выбор» («Множество»), а формы «Соответствие» и «Упорядоченный список» ¾ к форме «Упорядоченный список» («Список»). Отсюда следует, что для адекватной оценки результатов выборочного контроля знаний необходима разработка моделей и алгоритмов оценки ответов обучающихся, представленных в виде неупорядоченных и упорядоченных множеств элементов. Целесообразность использования для разработки моделей и алгоритмов оценки тестовых заданий в формах «Множество» и «Список» методов теории распознавания образов (Фор А., Фу К. ) обоснована в исследованиях И.П. Карповой.
Применение этих методов позволило предложить модели и алгоритмы оценки тестовых заданий в формах «Множество» и «Список», исключающие недостатки тех процедур оценки результатов тестирования, которые применяются в современных КСТ (Карпова И.П., Кумаритов А.М.). Однако предложенные процедуры не универсальны и обладают рядом недостатков. Так, например, предложенные (Карпова И.П.) модели и процедуры оценки тестовых заданий в форме «Список» корректны и работоспособны только при условии одинакового набора (числа и номенклатуры) элементов в сравниваемых списках. Модели и процедуры, приведенные А.М. Кумаритовым, вообще приводят к некорректным результатам, некорректность которых рассмотрены А.О. Туровской.
Однако, предложенный (И.П. Карпова) подход к решению задач оценивания результатов тестирования с применением методов теории распознавания образов представляется перспективным и требует дальнейшего развития.
Результаты анализа существа последних двух противоречий позволяют утверждать, что средством их разрешения является представление функция полезности как конечной формализованной формы представления системы предпочтений преподавателя в виде непрерывной функции. Для такого представления функции полезности могут рассматриваться два подхода.
Первый подход связан с внедрением в теорию и практику экспертных оценок методов теории нечетких множеств и нечеткой логики (Л. Заде). В современной литературе по экспертным оценкам (Железко Б. А., Морозевич А. Н., Кофман А., Хил Алуха Х., Недосекин А.О., Орлов А.И.), посвященной проблеме выявления качественных мнений экспертов, показано, что математического аппарата четких чисел для выражения знаний и мнений экспертов явно недостаточно. По мнению специалистов (Кофман А., Хил Алуха Х., Орлов А.И.) качественные знания экспертов можно формализовать только при привлечении аппарата теории нечетких множеств. Основой для проведения операции нечеткого логического вывода является база правил, содержащая нечеткие высказывания в форме «Если ¾ то» и функции принадлежности для соответствующих лингвистических термов (в нашем случае оценок вида «отлично», «хорошо» и т.д.).
В общем случае механизм логического вывода включает четыре этапа: 1) введение нечеткости (фазификация), 2) нечеткий вывод, 3) композиция, 4) приведение к четкости (дефазификация). Применительно к рассматриваемой процедуре оценивания результатов тестирования эти этапы имеют вид, приведенный на рис. 1.
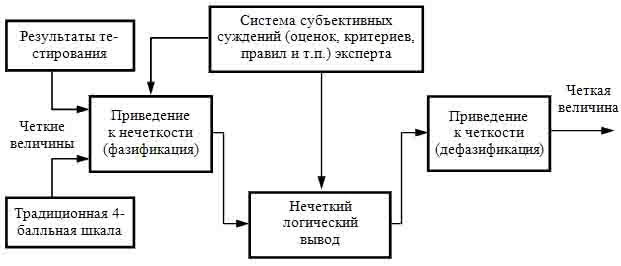
Рис. 1. Система нечеткого логического вывода.
Алгоритмы нечеткого вывода (Мамдани, Сугено, Ларсена, Цукамото) различаются главным образом видом используемых правил и разновидностью метода дефазификации. Однако применение любого алгоритмов не обеспечивает решения задачи дифференциации оценок уровня качества результатов тестирования. Недостаточность первого подхода для решения задачи оценивания результатов тестирования определяется тем фактом, что применение методов теории нечетких множеств и нечеткой логики позволяет оценить с помощью функции принадлежности лишь соответствие мнения эксперта тому или иному баллу традиционной 4-балльной шкалы, но не представить эту порядковую шкалу в виде интервальной. Другими словами, применение методов теории нечетких множеств и нечеткой логики не позволяет устранить дискретность оценок уровня подготовленности (учебных достижений) тестируемых.
Второй подход связан с определением функции полезности в виде аналитической зависимости. В педагогике, инженерной, педагогической и математической психологии, а также психофизике формулируется гипотеза о существовании некоторой единой, общечеловеческой системы предпочтений в отношении качества деятельности (знаний, квалификации и т.п.). В целом ряде работ, (Ратанова Т.А., Свиридов А.П.), приводятся различные закономерности оценок ЛПР, подтверждающие факт существования указанной общечеловеческой системы предпочтений.
В педагогике (Беспалько В.П.,
Печников А.Н., Свиридов А.П.) проблема формулировки системы
предпочтений обучающих в отношении подготовленности (учебных достижений)
обучающихся представлена как проблема выявления вида шкалы ![]() , где U — достигнутый
обучающимся результат, N — балл оценки в интервальной шкале, соответствующей
традиционной порядковой 4-балльной шкале, y
— функция гомоморфного отображения U в I (функция полезности). Целью
большинства проведенных исследований являлось именно выявление вида функции y, соответствующего системе предпочтений
обучающих в отношении качества учебной деятельности. В соответствии с результаты
экспериментальных исследований, сформулирован ряд закономерностей изменения
функции y (Печников А.Н.). Прежде
всего, установленным фактом необходимо считать, что формулируемые в ранговой
4-балльной шкале оценки обучающих («5 – отлично», «4 – хорошо», «3 –
удовлетворительно», «2 – неудовлетворительно») «устанавливают 4 класса
предпочтений на основании отношений типа «лучше» (правильнее, полнее)» (Турбович Л.
Т.), т.е. рассматриваются обучающими в качестве критерия качества и
эффективности деятельности обучающихся. Однако, в условиях обычной практики
обучения у каждого обучающего эти классы предпочтения и соответствующие им
ранги оценки не абсолютны. Например, экспериментально установлено (Суздаль В.
Г., Турбович Л. Т.], что на экзаменах более сильной и более слабых групп
одни и те же оценки по одной и той же шкале соответствуют не вполне равноценным
ответам обучающихся. При этом примерный интервал между оценками у одного и того
же обучающего сохраняется, т.е. сама оценка N может быть представлена функцией
, где U — достигнутый
обучающимся результат, N — балл оценки в интервальной шкале, соответствующей
традиционной порядковой 4-балльной шкале, y
— функция гомоморфного отображения U в I (функция полезности). Целью
большинства проведенных исследований являлось именно выявление вида функции y, соответствующего системе предпочтений
обучающих в отношении качества учебной деятельности. В соответствии с результаты
экспериментальных исследований, сформулирован ряд закономерностей изменения
функции y (Печников А.Н.). Прежде
всего, установленным фактом необходимо считать, что формулируемые в ранговой
4-балльной шкале оценки обучающих («5 – отлично», «4 – хорошо», «3 –
удовлетворительно», «2 – неудовлетворительно») «устанавливают 4 класса
предпочтений на основании отношений типа «лучше» (правильнее, полнее)» (Турбович Л.
Т.), т.е. рассматриваются обучающими в качестве критерия качества и
эффективности деятельности обучающихся. Однако, в условиях обычной практики
обучения у каждого обучающего эти классы предпочтения и соответствующие им
ранги оценки не абсолютны. Например, экспериментально установлено (Суздаль В.
Г., Турбович Л. Т.], что на экзаменах более сильной и более слабых групп
одни и те же оценки по одной и той же шкале соответствуют не вполне равноценным
ответам обучающихся. При этом примерный интервал между оценками у одного и того
же обучающего сохраняется, т.е. сама оценка N может быть представлена функцией ![]() , где, а — сдвиг.
Данный факт позволяет определить «принятую в педагогической практике балльную
шкалу как интервальную шкалу разностей предпочтения» (Турбович Л. Т.).
Кроме того, «индивидуальные оценочные шкалы обучающих на нижнем участке ориентированы
в сторону завышения отметок, а на верхнем — к занижению балла» (Мизенцев В.П.,
Кочергин А.В.). Последняя особенность индивидуальных оценочных шкал отмечается
практически во всех педагогических исследованиях, касающихся реализации процедуры
оценивания обучающими.
, где, а — сдвиг.
Данный факт позволяет определить «принятую в педагогической практике балльную
шкалу как интервальную шкалу разностей предпочтения» (Турбович Л. Т.).
Кроме того, «индивидуальные оценочные шкалы обучающих на нижнем участке ориентированы
в сторону завышения отметок, а на верхнем — к занижению балла» (Мизенцев В.П.,
Кочергин А.В.). Последняя особенность индивидуальных оценочных шкал отмечается
практически во всех педагогических исследованиях, касающихся реализации процедуры
оценивания обучающими.
Касаясь
вопроса взаимосвязи ![]() ,
следует считать установленным фактом, что данная взаимосвязь имеет нелинейный
характер (Мизенцев В.П., Кочергин А.В., Печников А.Н.). Другими
словами, если шкала U измерения результатов учебной деятельности имеет
аддитивную метрику, то соответствующая ей шкала оценки N — мультипликативную
метрику. Причем степень соответствия шкалы N и шкалы U имеет стабильный
характер, не зависит от вида осваиваемой области деятельности (учебной
дисциплины), а зависит только от уровня нормативных требований к степени ее
сформированности, т.е. от формулировки целей обучения. Данные, полученные на
основе различных способов измерения качества деятельности обучающихся
(Суздаль В.Г., Турбович Л.Т.), позволяют предполагать, что функция
,
следует считать установленным фактом, что данная взаимосвязь имеет нелинейный
характер (Мизенцев В.П., Кочергин А.В., Печников А.Н.). Другими
словами, если шкала U измерения результатов учебной деятельности имеет
аддитивную метрику, то соответствующая ей шкала оценки N — мультипликативную
метрику. Причем степень соответствия шкалы N и шкалы U имеет стабильный
характер, не зависит от вида осваиваемой области деятельности (учебной
дисциплины), а зависит только от уровня нормативных требований к степени ее
сформированности, т.е. от формулировки целей обучения. Данные, полученные на
основе различных способов измерения качества деятельности обучающихся
(Суздаль В.Г., Турбович Л.Т.), позволяют предполагать, что функция ![]() может иметь характер
логарифмической зависимости, функции Харрингтона или полиномиальной
зависимости. Конкретный вид зависимости определяется способом измерения
качества учебной деятельности обучающихся. Так приведенные данные (Турбович Л.Т.)
экспертной оценки большой группой обучающих (более 300 преподавателей)
специально разработанной системы тестов выявили, что функция y имеет характер логарифмической зависимости.
Этот вывод подтверждается (Молибог А.Г.), при этом предлагается
представлять соотношение N и U в виде
может иметь характер
логарифмической зависимости, функции Харрингтона или полиномиальной
зависимости. Конкретный вид зависимости определяется способом измерения
качества учебной деятельности обучающихся. Так приведенные данные (Турбович Л.Т.)
экспертной оценки большой группой обучающих (более 300 преподавателей)
специально разработанной системы тестов выявили, что функция y имеет характер логарифмической зависимости.
Этот вывод подтверждается (Молибог А.Г.), при этом предлагается
представлять соотношение N и U в виде ![]() , где U ¾
объем знаний материала в долях от 1. Данные эксперимента (Суздаль В.Г.,
Турбович Л. Т.), проведенного в условиях реального обучения, позволили сделать
вывод о возможности представления функции полезности как в виде логарифмической,
так и полиномиальной зависимости (параболы). Рассматривая вопрос преобразования
первичных тестовых баллов в оценку подготовленности (учебных достижений)
обучающихся, предлагается представлять соотношение N и U в виде
, где U ¾
объем знаний материала в долях от 1. Данные эксперимента (Суздаль В.Г.,
Турбович Л. Т.), проведенного в условиях реального обучения, позволили сделать
вывод о возможности представления функции полезности как в виде логарифмической,
так и полиномиальной зависимости (параболы). Рассматривая вопрос преобразования
первичных тестовых баллов в оценку подготовленности (учебных достижений)
обучающихся, предлагается представлять соотношение N и U в виде ![]() , где a, b, n –
коэффициенты, подлежащие определению (Ким В.С.).
, где a, b, n –
коэффициенты, подлежащие определению (Ким В.С.).
В психофизике
изучающей проблемы шкалирования человеком его физиологических реакций, вид
функции y прямо определяется выбором
соответствующего закона: 1) закона Фехнера, определяющего человеческую оценку R
ощущения в зависимости от интенсивности вызывающего это ощущение стимула S в виде
![]() , где: а —
коэффициент, S° — пороговое значение величины стимула S; 2) закона Стивенса,
определяющего ту же зависимость в виде
, где: а —
коэффициент, S° — пороговое значение величины стимула S; 2) закона Стивенса,
определяющего ту же зависимость в виде ![]() , где n — показатель степени, определяемый
экспериментально (обычно принимают п»0.5)
(Ратанова Т.А.). Выбор закона производится на основе данных о величине различия
рассматриваемых воздействий стимула: при малом различии на уровне пороговых
значений принимается закон Стивенса, а при большом различии — закон Фехнера.
Законы Фехнера и Стивенса определяют закономерности изменения человеческих
оценок в отношении интенсивности непосредственного воздействия на человеческий
организм различных сенсорных раздражителей (свет, температура и т.д.). Они не
распространяются на область сознательных оценок ЛПР, но рассматриваемые в психофизике
процессы субъективного шкалирования человеком его физиологических реакций,
несомненно, определяют и закономерности изменения тех человеческих оценок,
которые формируются в сознании человека.
, где n — показатель степени, определяемый
экспериментально (обычно принимают п»0.5)
(Ратанова Т.А.). Выбор закона производится на основе данных о величине различия
рассматриваемых воздействий стимула: при малом различии на уровне пороговых
значений принимается закон Стивенса, а при большом различии — закон Фехнера.
Законы Фехнера и Стивенса определяют закономерности изменения человеческих
оценок в отношении интенсивности непосредственного воздействия на человеческий
организм различных сенсорных раздражителей (свет, температура и т.д.). Они не
распространяются на область сознательных оценок ЛПР, но рассматриваемые в психофизике
процессы субъективного шкалирования человеком его физиологических реакций,
несомненно, определяют и закономерности изменения тех человеческих оценок,
которые формируются в сознании человека.
Однако приведенные выше модели представления функции полезности y не могут претендовать на адекватное отображение общечеловеческой системы предпочтений, поскольку не подтвердили свою валидность в нескольких не пересекающихся областях человеческой деятельности. Последнему требованию соответствует модель функции полезности и соответствующий ей метод оценки уровня качества, которые базируются на аксиоматике системно- информационного анализа (Горский Ю.М., Печников А.Н., Бугель Н.В., Кабанов А.А.). Эти модель и метод ориентированы на оценку квалификации специалистов различного профиля. Результаты проведенного выше анализа определяют целесообразность использования аксиоматики системно-информационного анализа и основных характеристик метода оценки уровня качества деятельности в процедуре критериально-ориентированного оценивания результатов тестирования.
Таким образом, результаты анализа подходов к разрешению противоречий в процедурах измерения и оценивания результатов критериально-ориентированного тестирования в современных КСТ позволяют предполагать, что оценка результатов критериально-ориентированного контроля знаний в компьютерных системах тестирования, будет объективной и дифференцированной, если модели и процедуры педагогического измерения и оценивания результатов тестирования будут основаны на методах теории распознавания образов и системно- информационного анализа.
Литература
1. Аванесов B.C. Композиция тестовых заданий. Учебная книга для преподавателей вузов, учителей школ, аспирантов и студентов педвузов. 4-е изд. - М.: Центр тестирования, 2002. - 237с.
2. Аванесов B.C. Методологические и теоретические основы тестового педагогического контроля знаний: Дисс. … докт. пед. наук. – СПб, 1994.-339с.
3. Беспалько В.П. Слагаемые педагогической технологии - М.: Педагогика, 1989. - 190с.
4. Бугель Н.В., Кабанов А.А. и др. Теоретические основы гомеостатического управления познанием: Монография / Под ред. А.Н. Печникова. – СПб: СПб ун-т МВД России, 2001. – 302с.
5. Горский Ю.М. Системно-информационный анализ процессов управления. - Новосибирск: Наука. Сиб. Отд-ние, 1988. – 268с.
6. Железко Б. А., Морозевич А. Н. Теория и практика построения информационно-аналитических систем поддержки принятия решений. - Мн.: «Армита - Маркетинг, Менеджмент», 1999. - 144 с.
7. Заде Л. Понятие лингвистической переменной и его применение к понятию приближенных решений.- М. Издательство «Мир».-1976.-169с.
8. Карпов В.Э., Карпова И.П. Язык описания системы контроля знаний // Компьютеры в учебном процессе, 2000, № 4. - с. 147-155.
9. Карпова И.П. Исследование и разработка подсистемы контроля знаний в распределенных автоматизированных обучающих системах: Дисс. … канд. техн. наук. – М.: МГИЭМ, 2002. – 239с.
10. Ким В.С. Тестирование учебных достижений: Монография. - Уссурийск: Издательство УГПИ, 2007. - 214 с.
11. Кофман А., Хил Алуха Х. Пошаговые методы принятия решений на моделях с неопределенностями / Пер. с исп. Под ред. В. В. Краснопрошина, Н. А. Лепишинского. – Минск: ООО «Скарына», 1995. – 259 с.
12. Кумаритов А.М., Дубенко Ю.В. Методы и алгоритмы контроля знаний и оценки эффективности автоматизированных обучающих систем на производственном предприятии // Аудит и финансовый анализ, 2009, №2, С. 455-467. URL: http://www.auditfin.com/fin/2009/3/11_01/11_01%20.pdf .
13. Мизенцев В.П., Кочергин А.В. Проблема аналитической оценки качества и эффективности учебного процесса в школе. - Куйбышев: Куйб. гос. пед. ин-т, 1986. - 112 с.
14. Молибог А.Г. Программированное обучение (вопросы научной организации педагогического труда). – М.: Высшая школа, 1967. -243 c.
15. Недосекин А.О. Методологические основы моделирования финансовой деятельности с использованием нечетко-множественных описаний: Дис. … док. экон. наук. – СПб.: СПбГУЭФ, 2003. – 286с. с сайта http://sedok.narod.ru/ .
16. Орлов А.И. Нечисловая статистика. - М.: МЗ-Пресс, 2004. - 345 с. с сайта http://orlovs.pp.ru/ .
17. Ратанова Т.А. Психофизиологические основы индивидуальности. – М.: МПСИ; МОДЭК, 2008. – 160с.
18. Ратанова Т.А. Субъективное шкалирование и объективные физиологические реакции человека / Научн.-исслед. ин-т общей и педагогической психологии акад. пед. наук СССР. – М.: Педагогика, 1990. – 216с.
19. Свиридов А.П. Основы статистической теории обучения и контроля знаний: Метод. пособие. - М.: Высшая школа, 1981. - 262с.
20. Суздаль В. Г., Турбович Л. Т. Контроль, диагностика, оценка знаний и эффективности обучения. - Л.: Изд. ЛДНТП, 1969. – 126с.
21. Турбович Л. Т. Информационно-семантическая модель обучения. - Л.: Изд-во ЛГУ, 1970. – 167с.
22. Туровская А.О., Туктаров Р.Р. Модели и процедуры оценки результатов компьютерного тестирования знаний // Образовательные технологии и общество (международный электронный журнал) – 2013. – Том 16. - №4. − C. 643 – 657 URL: http://ifets.ieee.org/russian/.
Поступила в редакцию 10.10.2013 г.