Методика определения границ «теневых» зон для одиночных препятствий в сотовых системах связи стандарта GSM
Галушко Олег Михайлович,
кандидат технических наук, доцент,
Коломбарь Денис Вадимович,
студент факультета информационных технологий.
Национальный горный университет, г. Днепропетровск, Украина.
В настоящее время строгой методики для определения границ «теневых» зон при распространении радиоволн с учетом влияния всех возможных факторов не существует
Из общего числа факторов, которые формируют зоны затенения, можно выделить три основных:
1) одиночные препятствия в виде зданий;
2) групповые, стоящие последовательно друг за другом по ходу распространения радиоволны;
3) интерференционные явления прямой и отраженной радиоволны.
Для одиночных препятствий в виде зданий обычно применяют аппроксимацию клиновидным препятствием. Такая аппроксимация справедлива в тех случаях, когда размеры препятствия вдоль трассы значительно меньше размера существенного эллипсоида для распространения в этом направлении, а поперек - значительно больше его поперечного размера, то есть условия дифракции соответствуют оптической дифракции Френеля.
Пусть между излучателем антенны базовой станции (БС), который находится на высоте hбс, и приемником – мобильной станцией (МС), который находится на высоте hмс, расположено препятствие в виде клина высотой hпр – рис. 1. Расстояние от точки прохождения линии излучения через препятствие до БС равно d1, а до МС – d2 . Расстояние от приемника МС до точки соприкосновения линии излучения с поверхностью земли равно ℓ, а угол между линией излучения и поверхностью земли составляет α. Расстояние от точки прохождения излучения через препятствие до его вершины равно h. В качестве приемника излучения рассматривается аьонент мобильгой связи, для которого средняя высота расположения абонентского устройства над землей принята равной 1,5 м.
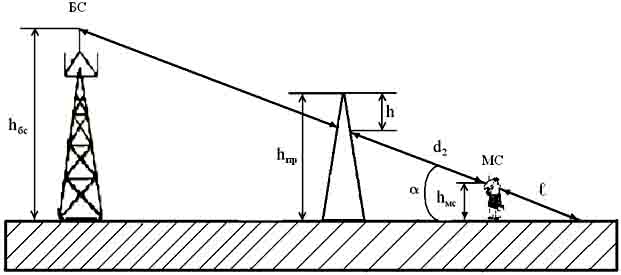
Рис. 1. Схема прохождения радиоволны, через одиночный клин.
Для приведенного рисунка справедливы следующие соотношения:
![]() (1)
(1)
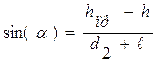 (2)
(2)
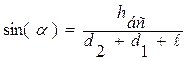 (3)
(3)
из которых следует:
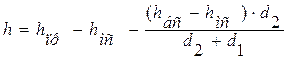 (4)
(4)
С другой стороны, безразмерный дифракционный параметр Френеля-Кирхгофа равен [2]:
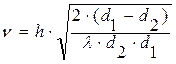 (5)
(5)
Таким образом, с учетом (4):
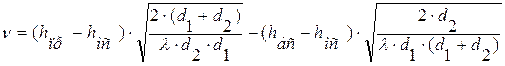 (6)
(6)
Коэффициент дифракционного усиления с препятствием по сравнению со свободным пространством [2]:
![]() , дБ. (7)
, дБ. (7)
А для ![]() приближенно
можно считать:
приближенно
можно считать:
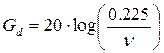 (8)
(8)
Для Gd = - 40 дБ (чему соответствует множитель ослабления V = 0.01), справедливо соотношение:
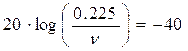 дБ
дБ
откуда безразмерный дифракционный параметр
Френеля-Кирхгофа:![]() .
.
Полученное выражение (6), в соответствии с принятым значением Gd, позволяет рассчитать ширину границы зоны затенения для принятой модели препятствия.
Однако, искомая ширина зоны затенения d2 представлена в (6) в неявном виде, что осложняет получение зависимостей этой величины от параметров hбс; hпр; d1, характеризующих процесс распространения радиоволн.
Практическую ценность может иметь аппроксимирующий многочлен, включающий параметры, оказывающие влияние на ширину зоны затенения d2 . Такой многочлен может быть получен, например, путем применения метода планирования эксперимента [3] для заданного числа независимых переменных, а именно, в данном случае – полный факторный эксперимент ПФЭ 23. При этом расчет значений d2 для узловых точек плана по выражению (6) удобно производить, например, с помощью пакета MathCad.
При решении поставленной задачи приняты следующие области определения факторов:
hбс = (20…40) м; hпр = (20…50) м; d1 = (300…1500) м.
В результате расчета коэффициентов уравнения регрессии, сокращения их числа за счет наименее значимых и замены переменой для фактора hпр получено следующее уравнение регрессии, аппроксимирующее реальную зависимость d2 = f(d1, hбс, hпр,):
При λ = 0,33 м - стандарт GSM – 900:
![]()
При λ = 0,158 м - стандарт GSM – 1800
![]()
Ошибка при вычислении значений d2 по полученным выражениям не превышает 10% по отношению к значениям, определенным по выражению (6).
Из анализа полученных уравнений следует, что фактором, оказывающим наименьшее влияние на ширину «теневых» зон является d1 – расстояние от рассматриваемого препятствия до базовой станции. Приняв это расстояние, равным 750 метров - среднему значению в указанном диапазоне, построены зависимости ширины теневых зон от двух других факторов. Одна из поверхностей отклика, а именно для λ = 0,33 м представлена на рис. 3.
Сечения полученных поверхностей, то есть зависимости d2 = f (hпр) для базовой станции высотой hбс = 30 м представлены на рис.4 - соответственно 1 – для стандарта GSM-900, 2 – для стандарта GSM-1800.
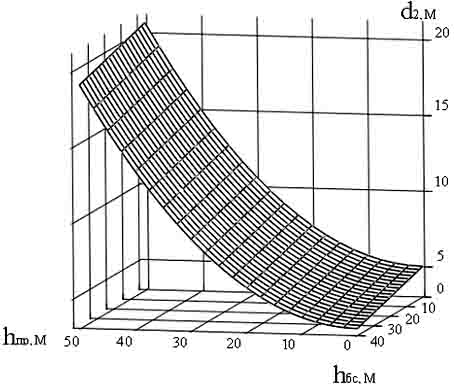
Рис. 3. Зависимость ширины «теневой» зоны от высот препятствия и базовой станции при расстоянии от БС до препятствия d1 = 750 м.
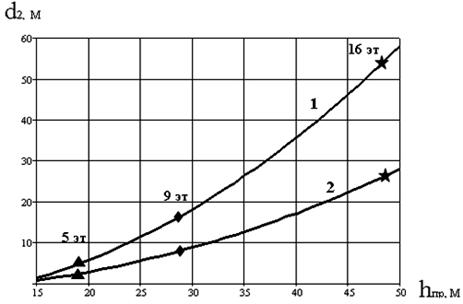
Рис. 4. Зависимости ширины «теневой» зоны от высоты препятствия.
Таким образом, в результате проведенных исследований получены удобные в практическом отношении зависимости для расчета ширины «теневой зоны» от отдельной станции в условиях городской застройки применительно к одиночным препятствиям, например, в виде зданий.
Литература
1. Богенс К.К., Ерохин Г.А., Шорин О.А. Прогнозирование теневых зон при расчете поля УКВ в системах подвижной радиосвязи // Электросвязь. – 2000.- N° 7.
2. Шабунин С.Н., Лесная Л.Л. Распространение радиоволн в мобильной связи. Методические указания по курсу «Распространение радиоволн и антенно-фидерные устройства в системах мобильной связи» для студентов всех форм обучения радиотехнических специальностей. Екатеринбург: УГТУ, 2000. – 38 с.
3. Ивоботенко В.А., Ильинский Н.Ф., Копылов И.П. Планирование эксперимента в электромеханике. – М.: Энергия, 1975. – 184 с.
Поступила в редакцию 29.04.2013 г.