Интерполяция траектории движения при контурном управлении с использованием полинома Лагранжа

Марахин Евгений Юрьевич,

Беляева Анастасия Сергеевна,

соискатели Омского государственного технического университета.

При обработке деталей на станках с ЧПУ в гибком автоматизированном производстве необходимо учитывать наличие у обрабатываемых деталей поверхностей сложного профиля, что характерно для деталей авиационной, ракетной, военной техники и в ряде других случаев [1]. В этом случае использование традиционных методов интерполяции (линейная, круговая) при контурном управлении обработкой малоэффективно.

Так, например, сложное описание имеют аэродинамические профили поверхностей самолета. В частности аэродинамический профиль NASA для крыла описывается зависимостью

где x – текущая координата точки профиля; t и C – постоянные параметры профиля.

Сложные профили характерны для деталей газотурбинных двигателей, компрессоров и подобной техники. При описании профилей деталей таких машин, часто используются полиномы различных степеней [2,3]. Например, для описания профиля лопатки компрессора предлагается использовать кривую Безье третьего порядка

,

где  – опорные точки, задаваемые их координатами, t – текущая относительная координата профиля.

При программировании обработки подобных поверхностей на станках с ЧПУ для обеспечения необходимой точности приходится увеличивать количество интерполяционных отрезков, снижать скорость обработки и увеличивать время обработки. Снизить отрицательное влияние перечисленных факторов можно за счет использования аппроксимации траектории движения обрабатывающего инструмента аналитическими кривыми, имеющими форму близкую к форме обрабатываемых участков детали.

Учитывая тот факт, что описание сложных профилей (в частности, аэродинамических) осуществляется, как правило, в табличной форме, представляет интерес использование для описания профиля полиномов Лагранжа, которые принимают данные значения в данном наборе точек интерполяции. Кроме этого полином Лагранжа позволяет использовать неравномерные интервалы между узлами интерполяции.

В качестве примера рассмотрим аэродинамический профиль NASA A-12%, заданный в таблице 1 [4].

Таблица 1.

Используем заданные в таблице точки в качестве углов интерполяции и определим интерполяционный полином Лагранжа по формуле Лагранжа:

 Log: = 2,135449444х – 52.81974858x² + 1050.2211x³ – 14342.57478x⁴+ +1.341115220*10⁵x⁵ – 8.743070670*10⁵x⁶+4.042189*10⁶x⁷‒1.3417935*10⁷x⁸+

+3.2174896*10⁷x⁹- 5.5639655*10⁷x¹⁰ +6.8571336*10⁷x¹¹ – 5.86362378*10⁷x¹²+ +3.30135319*10⁷x¹³ -1.099335256*10⁷x¹⁴ + 1.638765762*10⁶x¹⁵

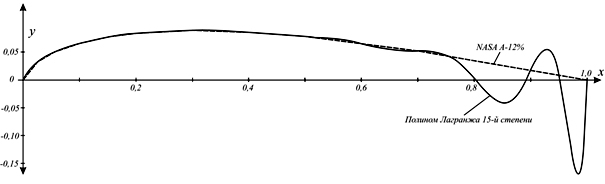
Рис. 1. Аппроксимация профиля NASA A-12% полиномом Лагранжа.

График профиля, соответствующего полученному полиному представлен на рис.1. Можно видеть, что конечная часть профиля описана явно неудовлетворительно. Такой результат можно было ожидать, поскольку, как правило, используют кусочную интерполяцию. Кроме этого из-за большого числа узлов получен полином 15-й степени, что усложняет его использование при расчетах.

Рассмотрим описание профиля по частям. Наиболее сложным является профиль носка в пределах х = 0 – 0,1. Составим для этого участка полином Лагранжа четвертой степени

Lag: = 1,909999999х – 31,54666660х² + 300,799999х³ – 1109,333330х⁴

Построение профиля выполнено на рис.2 а). При этом пунктирной линией показана кусочно-линейная аппроксимация профиля. График на рис. 2 показывает, что кривая, описываемая полиномом Лагранжа, проходит через базовые узлы и обеспечивает плавный характер профиля между узлами.

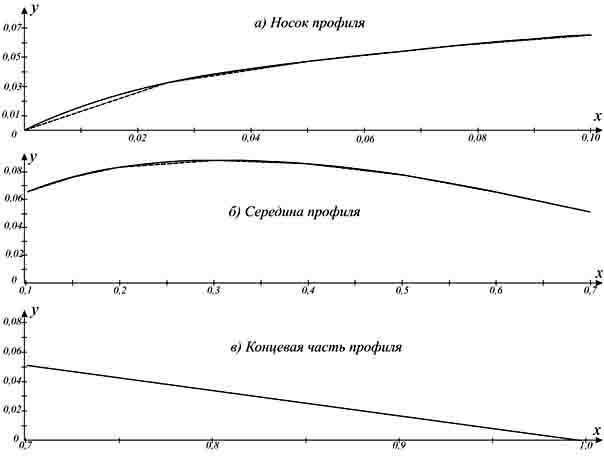
Рис. 2. Аппроксимация профиля по трем участкам.

Для среднего и концевого участков профиля были получены полиномы

Y₁ = - 16.64261672x⁷ + 44.93266012x⁶ – 47.83922576x⁵ + 24.86952870x⁴ – ‒5.736220563x³ – 0.3218249119x² + 0.4291476187x + 0.02938787880

Y₂ = 4.399999966x⁴- 14.82666656x³+ 18.61899987x²- 10.49743326x + +2.305099985

Графики этих участков представлены на рис. 2 б) и рис. 2 в), соответственно. Наблюдается хорошее совпадение заданного и интерполяционного профилей, что позволят рекомендовать рассмотренный способ интерполяции к практическому применению.

При управлении траекторией движения инструмента на станке с ЧПУ интерполяционный полином Лагранжа для соответствующего участка обработки используется в качестве оценочной функции. Для управления скоростью подачи инструмента необходимо контролировать вектор скорости, направление которого в системе координат станка задается производной от функции описания контура траектории [5]. Для полинома Лагранжа производная достаточно просто вычисляется. В нашем случае для носка профиля производная равна

dLag: = 1,909999999 – 63,09333320x + 902.399997x² – 4437.333320x³,

соответственно, производная легко вычисляется и для других участков профиля. Вычисленное значение производной в текущей точке интерполяции позволяет определить уставки для контуров регулирования скорости следящих координатных приводов

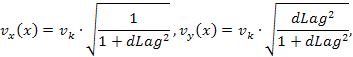
где v_x(x), v_y(x) – скорости координатных подач станка, v_k – заданная постоянная контурная скорость подачи при обработке.

Таким образом, использование полиномов Лагранжа при управлении обработкой на станках с ЧПУ возможно и представляет практический интерес вследствие простоты описания криволинейных участков траектории движения и возможности использования для описания таблично заданных профилей. Применение полиномов Лагранжа дает возможность удлинить интерполяционные отрезки траектории и приводит к сокращению объема управляющей программы.

Литература

1. Схиртладзе А.Г. Автоматизация технологических процессов и производств: Учебник/А.Г. Схиртладзе, А.В. Федотов. В.Г. Хомченко. – М.: Абрис, 2012. – 565 с.

2. Грушин М.А. Аппроксимация профилей лопаток компрессора с помощью кривых Безье / Наука и образование. Электронное научно-техническое издание. #07, июнь 2010. http://technomag.edu.ru/doc/147491.html.

3. Батурин О.В. Профилирование рабочих колес радиально-осевых турбин с помощью кривых Безье / Авиационная и ракетно-космическая техника. Вестник Самарского государственного аэрокосмического университета, №3(27). Часть 3. 2011. – С. 125 – 130.

4.  Перепечко С.А., Федотов А.В. Исследование системы контурного управления сверлильно-фрезерного станка / Автоматизация, мехатроника, информационные технологии: материалы III Международной научн. техн. Интернет-конференции молодых ученых. - Омск: Изд-во ОмГТУ, 2013.‒220 с.

5. Справочник авиационных профилей. http://kipla.kai.ru/liter/Spravochnic_avia_profiley.pdf.

Поступила в редакцию 26.11.2014 г.