О делимости чисел применительно к теореме Ферма
Карпунин Иван Иванович,
доктор технических наук, профессор, профессор Белорусского национального технического университета, академик Международной инженерной академии,
Подлозный Эдуард Дмитриевич,
кандидат технических наук, доцент, старший научный сотрудник ЧУО «БИП – институт правоведения», г. Минск.
Теорема 1. Число регулярных простых чисел бесконечно.
Пусть ![]() – произвольная конечная
система иррегулярных простых чисел. Теорема будет доказана, если мы найдем
иррегулярное простое число
– произвольная конечная
система иррегулярных простых чисел. Теорема будет доказана, если мы найдем
иррегулярное простое число
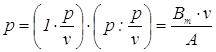 ,
,
отличное от ![]() . Где
. Где ![]() – регулярное простое;
– регулярное простое; ![]() – сомножитель (дробное число>1).
– сомножитель (дробное число>1). ![]() выбрано таким образом, что
выбрано таким образом, что ![]() >
>![]() .
. ![]() – число числителя чисел Бернулли,
– число числителя чисел Бернулли, ![]() – произведение регулярного числа
– произведение регулярного числа ![]() на
на ![]() ;
; 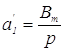 , где
, где ![]() – целое
число, полученное при делении числителя чисел Бернулли на иррегулярное число,
т. е.
– целое
число, полученное при делении числителя чисел Бернулли на иррегулярное число,
т. е. ![]() ;
; ![]() (
(![]() если не сокращать числитель и знаменатель).
если не сокращать числитель и знаменатель).
Предположим ![]() .
.
Так как для числа Бернулли ![]() мы
имеем [1]
мы
имеем [1]
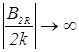 при
при ![]()
то при достаточно большом натуральном ![]() рациональное число
рациональное число ![]() будет
по абсолютной величине >1.
будет
по абсолютной величине >1.
Пусть ![]() – простое число,
входящее в его числитель (при несократимой записи). Если бы
– простое число,
входящее в его числитель (при несократимой записи). Если бы ![]() , то по теореме Штаудта [1], число
, то по теореме Штаудта [1], число ![]() входило бы в знаменатель
входило бы в знаменатель ![]() , а это не по выбору числа
, а это не по выбору числа ![]() . Следовательно,
. Следовательно, ![]()
![]() , а поэтому
, а поэтому ![]() отлично
от
отлично
от ![]() (и от 2). Обозначим через
(и от 2). Обозначим через ![]() остаток от деления
остаток от деления ![]() на
на ![]() , так
что
, так
что ![]() . Следует, что
. Следует, что ![]() –
четное и
–
четное и ![]() .
.
Вместе с ![]() число
число ![]() также не делится на
также не делится на ![]() . Воспользовавшись сравнением Куммера [1],
получим в кольце
. Воспользовавшись сравнением Куммера [1],
получим в кольце ![]() – целых рациональных чисел
сравнение
– целых рациональных чисел
сравнение
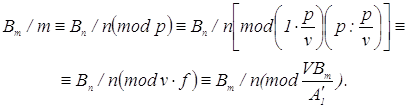
Используя сравнение по ненулевому рациональному модулю, доказано, что число простых регулярных чисел бесконечно.
Доказав вспомогательную теорему (1), «Если натуральное
нечетное составное число ![]() является произведением
двух простых чисел
является произведением
двух простых чисел ![]() и
и ![]()
![]() , то оно также является произведением третьего
простого числа натурального числа
, то оно также является произведением третьего
простого числа натурального числа ![]() на дробное число
на дробное число ![]() при
при ![]() или
или ![]() имеется частный случай (
имеется частный случай (![]() –простое число)» показано, что
–простое число)» показано, что
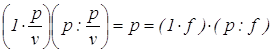 и
и ![]() .
.
Доказанная вспомогательная теорема (1) является подтверждением постулата Бертрана, означавшего, что для двух простых чисел найдется третье, которое больше обоих сомножителей, но меньше их произведения.
Для обоснования общей закономерности делимости чисел,
когда ![]() есть целое или дробное число (после
деления
есть целое или дробное число (после
деления ![]() на
на ![]() )
заметим, что любое натуральное число
)
заметим, что любое натуральное число ![]() делится на
делится на ![]() (при
(при ![]() )
независимо от того является ли число
)
независимо от того является ли число ![]() дробным или целым
дробным или целым ![]() .
.
Что касается простого целого иррегулярного числа ![]() , то это аналогично (что число
, то это аналогично (что число ![]() делится на
делится на ![]() ), где
), где
![]() – всегда дробное число
– всегда дробное число ![]() (при
(при ![]() ), где
), где ![]() - регулярное простое число. Число
- регулярное простое число. Число ![]() сравнимо по рациональному ненулевому
модулю.
сравнимо по рациональному ненулевому
модулю.
Известно, что ![]() [1-4];
но
[1-4];
но 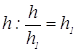 , где
, где 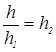 , т.
е.
, т.
е. ![]() делится на
делится на ![]() и
и ![]() .
.
Допустим, ![]() не делилось бы на
не делилось бы на ![]() , то и в этом случае
, то и в этом случае 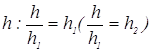 . Это означает, что независимо от того,
делится или не делится
. Это означает, что независимо от того,
делится или не делится ![]() на
на ![]() (является
или не является
(является
или не является ![]() произведением двух сомножителей
числа классов),
произведением двух сомножителей
числа классов), ![]() делилось бы на дробное число
>1, которое было бы нецелым.
делилось бы на дробное число
>1, которое было бы нецелым.
Аналогично, что если ![]() делится
на
делится
на ![]() , то в случае, если
, то в случае, если ![]() - иррегулярно, имеем
- иррегулярно, имеем ![]() (где
(где ![]() –
целое число от деления числителя чисел Бернулли
–
целое число от деления числителя чисел Бернулли ![]() на
иррегулярное число
на
иррегулярное число ![]() ). В случае, если
). В случае, если ![]() (где
(где ![]() –
дробное число >1 от деления чисел Бернулли
–
дробное число >1 от деления чисел Бернулли ![]() на
на ![]() , если оно было бы регулярным, то в обоих
случаях
, если оно было бы регулярным, то в обоих
случаях 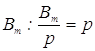 независимо от того,
независимо от того, ![]() делит
делит ![]() или не
делит. (
или не
делит. (![]() ).
).
Теорема 2. Если ![]() –
иррегулярное простое число, равное
–
иррегулярное простое число, равное ![]()
![]() , то между
, то между ![]() и
и ![]() содержится по меньшей мере одно
регулярное число
содержится по меньшей мере одно
регулярное число ![]() , равное
, равное ![]() .
.
Доказательство. Из литературы [1-4] известно, что число иррегулярных простых чисел бесконечно. Докажем, что число регулярных простых чисел также бесконечно.
Так как ![]() ,… то целое
,… то целое ![]() (где
(где 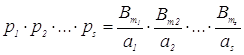 ,
, ![]() – числители чисел Бернулли,
– числители чисел Бернулли, ![]() – целые числа после деления
– целые числа после деления ![]() на
на ![]() ), очевидно
>1.
), очевидно
>1.
Предложение. Если ![]() делится
на
делится
на ![]()
![]() , то
независимо от того
, то
независимо от того ![]() дробное или целое число >1,
деление на это число дает целое число.
дробное или целое число >1,
деление на это число дает целое число.
Итак, имеем II случая: ![]() может
быть целым или дробным числом:
может
быть целым или дробным числом: ![]() – целым,
– целым, ![]() дробным большим 1.
дробным большим 1.
Частный случай I: ![]() –
целое число. Итак имеем
–
целое число. Итак имеем ![]()
![]() . Если
. Если ![]() делится
на
делится
на ![]() , то получается целое число, допустим
, то получается целое число, допустим ![]() . Тогда
. Тогда ![]() , где
, где ![]() .
.
Частный случай II. Здесь ![]() ,
, ![]() – дробное число >1. Представим дробное
число
– дробное число >1. Представим дробное
число ![]() следующим образом
следующим образом ![]()
![]() . Тогда
. Тогда ![]() ,
, ![]() .
.
В связи с тем, что ![]() (независимо
от того
(независимо
от того ![]() – дробное или целое число >1, как
частные случаи деления
– дробное или целое число >1, как
частные случаи деления ![]() на
на ![]() ), оно
(число
), оно
(число ![]() ) имеет делитель
) имеет делитель ![]() ,
который <
,
который <![]() , а следовательно, и <
, а следовательно, и <![]() . Если допустить, что
. Если допустить, что ![]() , то
, то ![]() будет
одним из сомножителей произведения:
будет
одним из сомножителей произведения: 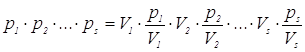 (где
(где ![]() может быть целым, или дробным числом (в
нашем случае
может быть целым, или дробным числом (в
нашем случае ![]() – дробное число >1) как частный случай
– дробное число >1) как частный случай
![]() ) и значит будет делителем произведения
) и значит будет делителем произведения ![]() . Но будучи делителем также числа
. Но будучи делителем также числа ![]() ,
, ![]() будет
делителем разности этих чисел, или числа
будет
делителем разности этих чисел, или числа ![]() , что
невозможно, так как
, что
невозможно, так как ![]() и
и ![]() .
Следовательно,
.
Следовательно, ![]() , а так как уже выяснено, что
, а так как уже выяснено, что ![]() , то имеем
, то имеем ![]() .
.
Так как 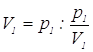 ,
, 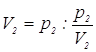 , …,
, …,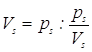 (где
(где ![]() ,
, ![]() ,…,
,…,![]() – также делители чисел
– также делители чисел ![]() ) и последовательность иррегулярных
простых чисел бесконечна, то получим последовательность простых регулярных
чисел:
) и последовательность иррегулярных
простых чисел бесконечна, то получим последовательность простых регулярных
чисел: ![]() количество которых также бесконечно. Это
означает, что теорема доказана.
количество которых также бесконечно. Это
означает, что теорема доказана.
Таким образом, для каждого иррегулярного числа существует регулярное большее его. Отсюда следует, что простых регулярных чисел бесконечное множество.
На основании выше изложенного, так как ![]() , поэтому
, поэтому ![]() и
и ![]() . Так как
. Так как ![]() здесь
равно одному из чисел
здесь
равно одному из чисел ![]() (
(![]() ;
; ![]() ;
; 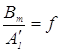 ;
; ![]() ) и так как
) и так как ![]() (где
(где ![]() делится на
делится на ![]() независимо
от того
независимо
от того ![]() дробное или целое число >1 и по
следствию теоремы [1] число
дробное или целое число >1 и по
следствию теоремы [1] число ![]() – иррегулярное и их
число бесконечно, то на основании того, что
– иррегулярное и их
число бесконечно, то на основании того, что ![]() , где
, где
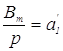 ;
; ![]() ,
, ![]() – целое число,
– целое число, ![]() – число
с остатком после деления
– число
с остатком после деления ![]() на
на ![]() и
и ![]() , и
теоремы 2 доказано, что число регулярных простых чисел также бесконечно. Этим
все сказано как о подлинности теоремы П. Ферма, так и о бесконечности
регулярных простых чисел. На основании полученных результатов и имеющихся
литературных источников предлагается следующее.
, и
теоремы 2 доказано, что число регулярных простых чисел также бесконечно. Этим
все сказано как о подлинности теоремы П. Ферма, так и о бесконечности
регулярных простых чисел. На основании полученных результатов и имеющихся
литературных источников предлагается следующее.
1. Доказать, что не найдется таких значений x,y,m,n, где х≠у≠0. m≠n, при которых равенство хm =yn выполняется, m,n≥5, x,y,m,n - простые нечетные числа.
2. Доказать, что числа 2n-1 и 2n+1 не могут оба быть одновременно простыми при простом n, где n≥3.
3. Доказать, может ли число 2n+1 быть простым при простом n, где n≥11 (при n=11 число 2n +1 делится на 3).
4. Доказать, имеет ли решения в целых числах уравнение nxn +mym=zp, если х≠у≠0,m≠n≠p, m,n,p≥3, m,n,p–простые числа.
5. Доказать, имеет ли решения в целых числах уравнение nxn +mym=рzp, если х≠у≠0,m≠n≠p, m,n,p≥3, m,n,p–простые числа.
6. Доказать, делятся ли о числа 2n-1 и 2n+1 (при определенном значении n) на n, где n-простое число, n≥5.
7. Доказать, является ли число 2m+2n+1 простым при простых m,n (m≠n).
8. Доказать, является ли число 1+2+23+25+27+211+….+2n простым, где n-простое нечетное число.
Литература
1. Боревич З.И., Шафаревич Н.Р. Теория чисел. М.: Наука.–1985.– 368 с.
2. Постников М.М. Введение в теорию алгебраических чисел. М.: – 1980. –Наука– 239 с.
3. Эдвардс Г. Последняя теорема Ферма. М.: Мир.–1980.– 480 с.
4. Карпунин И.И., Подлозный Э.Д. К вопросу о делимости чисел / Сучаснi проблеми науки та освiти. 8-а Мiжнародна мiждисциплiнарна науково-практична школа-конференцiя. Харькiв – 2007. – С. 80.
Поступила в редакцию 23.12.2013 г.