Бинарная потоковая последовательность – не Марковский процесс выпадения монеты. Бинарные слова и треугольник Паскаля
Филатов Олег Владимирович,
инженер-программист НТЦ Модуль, г. Москва.
Активный физический процесс, параметры которого при измерении дополняются различными логическими условиями, можно описать разными, взаимно не связанными формулами. Физический процесс выпадения монеты описывается двумя способами, разными формулами.
Структура бинарных слов сравнивается со структурой последовательности из бесконечного числа выпадений монеты и с треугольником Паскаля.
Ключевые слова: граф, рёбра графа, потоковая последовательность, составное событие, монета, выпадение монеты, Марковский процесс, треугольник Паскаля.
Используемые сокращения и термины: ф.; ф-ла – формула.
Выпадения монеты в Марковском процессе
Марковский процесс – это случайный процесс, в котором «будущие» события зависят от текущего состояния и не зависят от предшествующих состояний.
Вот описание Марковского процесса с подбрасыванием монеты.
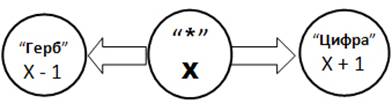
Рис. 1. Граф перемещения Марковской точки из положения х, после выпадения монеты.
Вдоль оси с делениями случайным образом перемещается точка. В начале, точка находится в нулевой координате оси. Бросается монета. Если выпал герб, то точка перемещается на одну позицию вправо, если цифра — перемещается на одну позицию влево. Любой бросок монеты приводит к перемещению точки, зависящему от выпавшей стороны монеты. Процесс изменения положения точки («блуждания») представляет собой случайный процесс со счётным множеством состояний. Такой случайный процесс называется Марковским, так как следующее состояние точки зависит только от настоящей (текущей) координаты X и не зависит от прошлых состояний (неважно, каким путем и за какое время точка попала в текущую координату). После следующего броска монеты в зависимости от результата выпадения (герб, цифра) точка окажется либо в координате X+1, либо в координате X-1.
Текущую сторону монеты не нужно знать для будущего перемещения точки. Будущее положение точки на оси определяется её текущим положением на оси. Результат выпадения монеты в данном эксперименте является лишь указателем направления для дискретного перемещения точки из текущего положения x. Поэтому в графе, на рисунке 1, состояние монеты обозначено как “*”. А X – текущая координата точки на оси.
Случайные блуждания точки, по результатам выпадений монеты, возле первичного положения точки доказывает равную вероятность выпадения герба и цифры при большом числе бросков монеты.
Описание не Марковского процесса «Потоковая последовательность»
На рисунке 2 представлен граф выпадения событий «Потоковой последовательности», описывающий выпадение сторон монеты в не Марковском процессе.
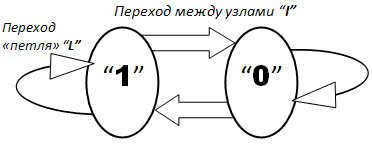
Рис. 2. Граф выпадения сторон монеты в эксперименте «Потоковая последовательность».
Обозначим выпадение герба монеты «1», а цифры «0». Каждый результат подбрасывания монеты дописываем в продолжение ранее выпавшему результату. Получаем цепочку результатов выпадения монеты, примерно, как в примере 1.
Пример 1: 10110110011001111001000101011111001010011…
Выпадение любой из сторон монеты не связано с другими действиями (кроме последовательных записей результатов выпадения сторон).
Но, для построения графа, рис.2, описывающего выпадение сторон монеты в потоковой последовательности, необходимо знать, результат выпадения предыдущего броска монеты. Только при знании предыдущего состояния монеты текущее выпадение можно квалифицировать на графе как «петлю», или как инверсию. Петля на рис.2 обозначает повторенное выпадение той же стороны, как и в предыдущем броске. «Переход между узлами» (инверсия) на рис.2 обозначает выпадение другой стороны монеты, не такой как в предыдущем броске.
То есть, в отличие от Марковского процесса, рис.1, в графе которого для получения нового значения выпадения монеты не нужно знать текущее состояние, для построения графа на рис.2, значение последней выпавшей стороны монеты (текущее состояние) надо знать.
Сравнение ключевых моментов хранения информации о результатах выпадения монеты, для Марковского процесса («Блуждание точки» по воле монеты) и не Марковского процесса («Потоковая последовательность» - результатов выпадения монеты), дано в таблице 1.
Таблица 1.
|
№№ |
Пункты сравнения случайных бинарных процессов |
Марковский процесс |
Потоковая последовательность (процесс) |
|
1 |
Связь последующего выпадения монеты с текущим состоянием монеты |
Нет связи |
Нет связи |
|
2 |
Связь последующего состояния системы с её текущим состоянием |
Есть, последующее положение точки на оси зависит от текущего положения точки на оси |
нет |
|
3 |
Сохранность информации о текущем состоянии монеты |
После установления текущего состояния информация о состоянии монеты забывается |
Сохраняется, дописываясь вслед за предыдущим результатом |
|
4 |
Необходимость знания текущего состояния монеты для рисования графа событий монеты |
Не надо знать текущее состояние монеты, граф без петель (рис.1) |
Надо знать текущие состояние монеты, граф с петлями (рис.2) |
|
5 |
Необходимость знания всех выпадений монеты в обработке результата эксперимента |
Нет, не нужно хранить историю выпадений монеты |
Да, история выпадений и есть сама потоковая последовательность |
Таким образом, исходя из таблицы 1, «Потоковую последовательность» можно определить как память о результатах выпадения монеты. И в связи с этим определением («Потоковая последовательность» - это память) особенно интересно отметить, что формула, описывающая выпадение повторных состояний монеты «111..» («петля» на рис.2) другая, чем формула описывающая выпадение инверсных событий типа «101010..» (ребро - «Переход между узлами» на рис.2).
Любая потоковая последовательность (пример 1) может быть разложена на составные события. И любая потоковая последовательность является объединением составных событий различных мод [1, 2, 3]. В работах [1, 2] вводится ф. 1, описывающая разложение любой потоковой последовательности на составные события nS:
![]() (1)
(1)
где n – длина составного события, n = 1, 2, 3, …; N – число бросков монеты.
Для того, что бы убедиться в работоспособности (1) по выпадению составных событий [1, 2], достаточно сто раз подбросить монету, N=100. Но для изучения открытых новых законов для потока выпадающих монет, N должно быть более 103 бросков, число составных событий nS всех мод растёт вместе с ростом бросков монеты.
Примеры составных событий приведены в таблице 2.
Таблица 2.
|
|
|
|
|
|
|
|
«0», «1» |
«00», «11» |
«000», «111» |
«0000», «1111» |
«00000», «11111» |
«0 .. 0n», «1 .. 1n» |
Показано [1, 2], что сумма всех составных событий последовательности Число составных событий S равно половине числа бросков монеты N:
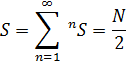 (2)
(2)
Стрелочка «à» обозначает переход
между узлами графа рис.2. Но узлы графа являются составными событиями потоковой
последовательности и стрелочка «à» есть переход от одного составного события к другому
составному событию: “000” à
”1” à ”00” à ”1111” à … ![]() . Так как
переходы между составными событиями и рёбра графа «переход между узлами» одно и
то же, то их численность одинакова. И по (2) равна
. Так как
переходы между составными событиями и рёбра графа «переход между узлами» одно и
то же, то их численность одинакова. И по (2) равна ![]() .
.
Таким образом, по (2) рассчитывается как число составных событий, так и число рёбер графа типа «переход между узлами». (3) учитывает, что число переходов I(S) на один меньше, чем число S (“000”à”1”à”00” – три составных события и два перехода между ними):
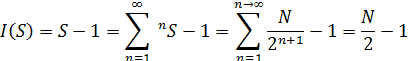 (3)
(3)
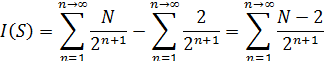 (3.1)
(3.1)
nI(nS) – число «Переходов между узлами» (математическое ожидание), рис.2, после выпадения n-раз подряд монеты (например: n=3; “111à0”, ”000à111”), зависит от длины последнего составного события в потоковой последовательности. Очевидно, что если его длина не равна n, то nI(nS) рассчитывается (3.2). Если длина последнего события потоковой последовательности равна n, то (3.3):
![]() (3.2)
(3.2)
![]() (3.3)
(3.3)
Частоты применения формул (3.2) и (3.3) зависит от частоты встречания nS в потоковой последовательности, которая рассчитывается по (1).
При расчёте петель, рис.2, учитываются последовательные выпадения однотипных элементарных событий, типа: «000», «11». Рассмотрим переход типа «петля», рис.2, на примере составного события пятой моды 5S: «11111» (пять элов подряд, смотри работы [1, 2]). Обозначим переход типа петля большой английской буквой L (от английского слова Loop), и стрелочкой «à». Тогда у пяти единиц выпавших подряд будет четыре перехода типа «петля»: «1à1à1à1à1». Можно обобщить – число переходов m типа петля внутри составного события nS будет на единицу меньше числа элов n[1,2], составляющих это составное событие nS:
m = n – 1 (4)
Число переходов типа «петля» L(S), изображённых на рис.2, будет рассчитываться внутри всей потоковой последовательности из (1) по (5):
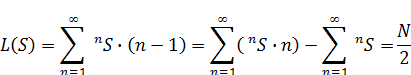 (5)
(5)
В (5.1) составные события nS выражены через (1):
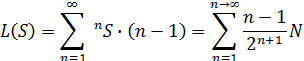 (5.1)
(5.1)
В конечных длинных потоковых последовательностях, пример 1, число переходов типа «петля» L(S) на один переход больше, чем инверсных перехода I(S):
L(S) = 1 + I(S) (6)
Формула 6 показывает асимметрию между двумя типами рёбер в графе рис.2, для «процесса потоковая последовательность.
Так как: ![]() , (5); а
, (5); а ![]() , (3), то перепишем
равенство (6), используя (5) для подсчёта числа рёбер графа L(nS) типа «петля», и
используя
(3)
для подсчёта
числа рёбер графа I(nS) типа «переход
между узлами», в виде (7.1):
, (3), то перепишем
равенство (6), используя (5) для подсчёта числа рёбер графа L(nS) типа «петля», и
используя
(3)
для подсчёта
числа рёбер графа I(nS) типа «переход
между узлами», в виде (7.1):
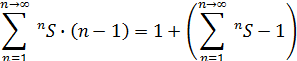 (7.1)
(7.1)
Раскрывая nS в (7.1) по (1), получаем (7.2):
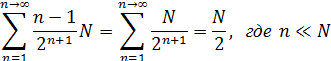 (7.2)
(7.2)
Формулы (3.1) и (5.1) показывают, что переходы (рёбра) графа, рис.2, описываются двумя бесконечными рядами: L(S) – рядом петель и I(S) – рядом переходов (инверсий) между вершинами. При стремлении n и N к большим величинам, сумма членов обоих рядов (L(S) и I(S)) стремится к одной и той же величине – N/2, (7.1) и (7.2). Что означает в пределе равенство сумм членов этих рядов.
При любых конкретных значениях n и N суммы рядов L(S) и I(S) взаимно отличаются на математически рассчитываемую величину. Что означает разную вероятность в переходах по рёбрам графа на рис.2, для nS - составных событий n-й моды. Вероятность выпадений монеты той же самой стороной будет отличаться от вероятности выпадения монеты другой стороной. Хотя при стремлении к бесконечному числу бросков рассчитываемые вероятности «петель» и «переходов», рис.2, стремятся к одной и той же величине: р = (N/2) : N = 0,5.
Сумма вероятностей переходов по рёбрам графа, рис.2, для всех мод nS составных событий стремится к единице при числе бросков монеты N стремящимся к бесконечности, (8). Для написания формулы (8) используем полученное равенство в (7.2):
![]() (8)
(8)
Представляя L(S)+I(S) в виде суммы рядов ((5.1) и (3.1)), и производя преобразования, получаем равенство (8.1):
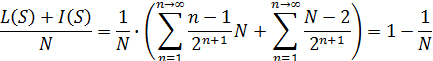 (8.1)
(8.1)
Величины математических ожиданий выпадения подряд, друг за другом, однотипных событий графа рис.2, рассчитывается для членов ряда L(S) по формуле (5.1), а для I(S) по формуле (3.1). Графики математических ожиданий для N=103 приведены на рис.3. Так, в тысячи выпадений монеты ожидается 62 серии содержащих по три инверсионных событий графа I(3). Но ожидается 125 серий по три ребра графа типа петля L(3).
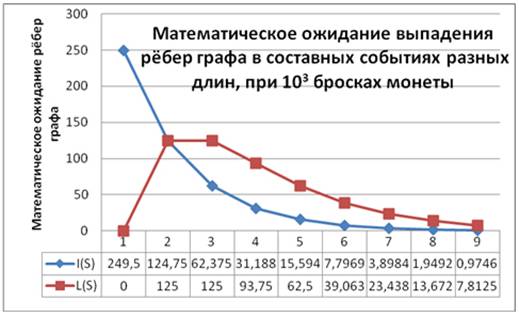
Рис. 3. Графики математических ожиданий для N=103.
Из рис. 3 видно, что только для L(2S) и I(2S) математическое ожидание числа переходов (рёбер) в графе, рис.2, почти равно между собой. Остальные точки графиков L(S) и I(S) отличаются друг друга.
Сравним законы выпадения монеты в потоковой последовательности с законами в комбинаторном распределении. Перейдём от длинных потоковых последовательностей, пример 1, к n-разрядным бинарным словам. В n-разрядном бинарном слове (спектре): «123..n», вместо цифр, обозначающих порядковый номер разряда в слове нули и единицы: «10101», «111».
Граф на рис.2 описывает выпадения монет в n-разрядных бинарных словах и в потоковой последовательности. Переходы графа типов: «петля» и «переход между узлами» изучим в таблице 3, на примере восьми трёх разрядных (n=3) слов.
Таблица 3.
«Комбинаторные распределения».
|
№ |
Слова |
Тип перехода в графе на рис.2 |
|||||||||
|
«I» |
«L» |
||||||||||
|
|
|
|
|
(«0à1»,«1à0») |
0 |
1 |
2 |
(«0à0»,«1à1») |
0 |
1 |
2 |
|
1 |
0 |
0 |
0 |
0 |
* |
|
|
2 |
|
|
* |
|
2 |
0 |
0 |
1 |
1 |
|
* |
|
1 |
|
* |
|
|
3 |
0 |
1 |
0 |
2 |
|
|
* |
0 |
* |
|
|
|
4 |
0 |
1 |
1 |
1 |
|
* |
|
1 |
|
* |
|
|
5 |
1 |
0 |
0 |
1 |
|
* |
|
1 |
|
* |
|
|
6 |
1 |
0 |
1 |
2 |
|
|
* |
0 |
* |
|
|
|
7 |
1 |
1 |
0 |
1 |
|
* |
|
1 |
|
* |
|
|
8 |
1 |
1 |
1 |
0 |
* |
|
|
2 |
|
|
* |
|
9 |
|
|
|
∑I=8 |
|
∑L=8 |
|
||||
|
10 |
|
Двойной |
2 |
4 |
2 |
Двойной |
2 |
4 |
2 |
||
В таблице 3 сравниваются между собой два типа рёбер графа с рис.2. Рассматривается трёхразрядное слово (n=3). В трёх разрядах возможно образовать восемь различных слов: «000», «001», …, «111» - столбцы «Слова» в таб. 3. Но всё описываемое в таб. 3 будет верно для слов любой разрядности (n>0).
В строке анализируется слово «000». В слове «000» нет ни одной инверсии (превращения нуля в единицу и наоборот). Поэтому в столбце «I» (переходы между вершинами графа, рис.2), стоит цифра 0, ноль переходов. А звёздочка «*» стоит в столбце с номером 0.
В группе столбцов «L» рассматриваются переходы графа типа «петля», рис.2. В слове «000» таких перехода два – цифра 2 стоит в столбце «L». И звёздочка «*» стоит в столбце с номером 2.
В строке №9 суммы рёбер по столбцам «I», «L» - они одинаковые.
В строке №10 подсчитаны звёздочки. Оказывается их раскладка по числу рёбер графа (2, 4, 2) является n-ой строкой паскале-подобного треугольника, таблица 4, значения строк которого рассчитываются по (9):
![]() (9)
(9)
![]()
где: n – число разрядов в бинарном слове; r – число рёбер в графе, рис.2.
То есть по (9) можно рассчитать, сколькими способами L(r,n) = I(r,n) в n-разрядном слове можно разместить r переходов типа L «петля» (1111 – три перехода), или типа I «инверсия» (101010 – пять переходов).
В таблице 4
приведены без скобочек значения, полученные из n-разрядных бинарных слов (рассчитанных
по (9) рёбер графа, рис.2). В скобочках – вершины ![]() Паскаля. В скобочках
числа
Паскаля. В скобочках
числа ![]() Паскаля. Числа
без скобочек образованы из n–разрядных бинарных слов по (9).
Паскаля. Числа
без скобочек образованы из n–разрядных бинарных слов по (9).
В таблице 5 показано образование строк треугольника Паскаля из n-разрядных бинарных слов.
Таблица 4.
«Вершина ![]() Паскаля».
Паскаля».
|
|
|
|
|
|
|
|
|
|
|
∑ |
∑ ( |
|
n=1 |
2(1) |
|
|
|
|
|
|
|
|
2 |
(1) |
|
n=2 |
2(1) |
2(1) |
|
|
|
|
|
|
|
4 |
(2) |
|
n=3 |
2(1) |
4(2) |
2(1) |
|
|
|
|
|
|
8 |
(4) |
|
n=4 |
2(1) |
6(3) |
6(3) |
2(1) |
|
|
|
|
|
16 |
(8) |
|
n=5 |
2(1) |
8(4) |
12(6) |
8(4) |
2(1) |
|
|
|
|
32 |
(16) |
|
n=6 |
2(1) |
10(5) |
20(10) |
20(10) |
10(5) |
2(1) |
|
|
|
64 |
(32) |
|
n=7 |
2(1) |
12(6) |
30(15) |
40(20) |
30(15) |
12(6) |
2(1) |
|
|
128 |
(64) |
|
n=8 |
2(1) |
14(7) |
42(21) |
70(35) |
70(35) |
42(21) |
14(7) |
2(1) |
|
256 |
(128) |
|
n=9 |
2(1) |
16(8) |
56(28) |
112(56) |
140(70) |
112(56) |
56(28) |
16(8) |
2(1) |
512 |
(256) |
Таблица 5.
Образование ![]() Паскаля.
Паскаля.
|
№ |
Слова |
|
Число полярных составных событий первой моды (n=1) |
||||||||||
|
|
n=1S1 |
|
n=1S0 |
||||||||||
|
|
0 |
1 |
2 |
3 |
Ось симметрии |
0 |
1 |
2 |
3 |
||||
|
1 |
0 |
0 |
0 |
|
* |
|
|
|
|
|
|
* |
|
|
2 |
0 |
0 |
1 |
|
|
* |
|
|
|
|
* |
|
|
|
3 |
0 |
1 |
0 |
|
|
* |
|
|
|
|
* |
|
|
|
4 |
0 |
1 |
1 |
|
|
|
* |
|
|
* |
|
|
|
|
5 |
1 |
0 |
0 |
|
|
* |
|
|
|
|
* |
|
|
|
6 |
1 |
0 |
1 |
|
|
|
* |
|
|
* |
|
|
|
|
7 |
1 |
1 |
0 |
|
|
|
* |
|
|
* |
|
|
|
|
8 |
1 |
1 |
1 |
|
|
|
|
* |
* |
|
|
|
|
|
9 |
1S=10 |
|
1 |
3 |
3 |
1 |
1 |
3 |
3 |
1 |
|||
|
10 |
2S=4 |
|
|
|
|||||||||
Оказывается, что
![]() Паскаля
образуется из полярных составных событий [1, 2] первой моды в пространстве
n-разрядного слова.
Паскаля
образуется из полярных составных событий [1, 2] первой моды в пространстве
n-разрядного слова.
Так в строке №1 со словом «000» нет ни одного единичного события S1 (единичное полярное составное событие первой моды), поэтому в разделе n=1S1 для строки №1 звёздочка стоит в столбце «0». В то же время, в слове «000» целых три события S0 (нулевое полярное составное событие первой моды). Поэтому в разделе n=1S0 для строки №1 звёздочка стоит в столбце «3».
И так далее для всех остальных трёхразрядных строк. В строке №9 суммируются звёздочки по столбцам. Полученные числа являются числами из треугольника Паскаля.
Строки треугольника Паскаля получается и из нулевых и из единичных полярных событий первой моды n - разрядных слов. И обе области построения в таблице 5, симметричны относительно табличного столбца симметрии.
Образование треугольника Паскаля из бинарных слов требует введение нулевых составных событий: 0S1 и 0S0, так как существуют столбцы «0» в которых подсчитываются состояния, в которых отсутствуют полярные составные события. Обозначим как: 0S1– единичное (1), 0S0 –нулевое (0) полярное составное событие нулевой длины.
Формально можно посчитать численность составных событий нулевой длины 0S в потоковой последовательности. По (1) более коротких событий (длина n-1) в два раза больше, чем длинных (n). Отсюда:
![]() (10)
(10)
Предположив, что полярных составных событий 0S1 и 0S0 поровну, получаем формулу (10.1) для расчёта их численности:
![]() (10.1)
(10.1)
Составные события
первой моды образующие ![]() Паскаля,
вызывают ассоциацию с
работой [5]. В работе производилось привязка разговорных языков к единой
цифровой лингвистической оси. Процедура помещения разговорного языка на
лингвистическую ось была сходна с описанным в этой статье образованием
треугольника Паскаля из n-разрядного бинарного слова. А именно, в каждом из
разговорных языков выявлялось число составных событий первой моды (и находилось
отношение составных событий первой моды к числу букв исследуемого языкового
фрагмента).
Паскаля,
вызывают ассоциацию с
работой [5]. В работе производилось привязка разговорных языков к единой
цифровой лингвистической оси. Процедура помещения разговорного языка на
лингвистическую ось была сходна с описанным в этой статье образованием
треугольника Паскаля из n-разрядного бинарного слова. А именно, в каждом из
разговорных языков выявлялось число составных событий первой моды (и находилось
отношение составных событий первой моды к числу букв исследуемого языкового
фрагмента).
Числам из треугольника Паскаля можно придать смысл, так как эти числа совпадают с распределением рёбер графа на рис.2, то треугольник Паскаля может рассматриваться как результат распределения выпадения сторон монеты, вернее как результат проявления случайных бинарных событий с вероятностью 0,5.
В таб. 5 числа треугольника Паскаля получались как суммы полярных составных событий [1, 2] первой моды в пространстве n-разрядных слов. Будем искать в бинарном слове все составные события (а не только полярные) одинаковой длины, на примере трёх разрядных строк таб. 5.
В строке №9, таб.5, есть запись «1S=10» - это все события единичной моды, посчитанные во всех трёхразрядных словах. В строке 1 этих событий нет. В строке 2 есть одно событие – «1». В строке три целых три события: «0», «1», «0». И т.д. В трёхразрядных словах будет 10 единичных событий, таб. 6, клетка: W(n=3); 1S.
В строке №10, таб.5, есть запись «2S=4» - это все события второй моды, посчитанные во всех трёхразрядных словах. В строке 1 этих событий нет. В строке 2 есть одно событие – «00». В строке три этих событий нет. В строке 4 есть одно событие – «11». И т.д. В трёхразрядных словах будет 4 двойных события, таб. 6, клетка: W(n=3); 2S.
Распределение всех составных событий одинаковой длины (а не только полярных) в n-разрядных бинарных словах дано в таблице 6, рассчитанных по ф.11. Символ W - означает бинарное слово длины n. В строка W(n= ) указаны длины бинарных слов. В строках 1S, 2S, … , nS – содержатся составные события указанной длины (1, 2, …, n).
Таблица 6.
Составные события n-разрядных слов.
|
W(n= ) |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
1S |
2 |
4 |
10 |
24 |
56 |
128 |
288 |
640 |
1408 |
|
2S |
|
2 |
4 |
10 |
24 |
56 |
128 |
288 |
640 |
|
3S |
|
|
2 |
4 |
10 |
24 |
56 |
128 |
288 |
|
4S |
|
|
|
2 |
4 |
10 |
24 |
56 |
128 |
|
5S |
|
|
|
|
2 |
4 |
10 |
24 |
56 |
|
6S |
|
|
|
|
|
2 |
4 |
10 |
24 |
|
7S |
|
|
|
|
|
|
2 |
4 |
10 |
|
8S |
|
|
|
|
|
|
|
2 |
4 |
|
9S |
|
|
|
|
|
|
|
|
2 |
Примеры определение числа составных событий в бинарном n- разрядном слове по таблице 6.
В бинарном пятиразрядном слове надо найти число составных событий единичной длины (заметим, на длине 5 разрядов возможно 32 не повторяющихся слова и поиск ведётся в каждом из них). На пересечении столбца имеющего заголовок «5» (длина бинарного слова) и строки 1S (составные события единичной длины) находится число 56. Столько составных событий единичных длин размещаются не повторяющимся образом в 5-разрядных словах.
В бинарном пятиразрядном слове надо найти число составных событий троичной длины. На пересечении столбца имеющего заголовок «5» (длина бинарного слова) и строки 3S (составные события троичной длины) находится число 10. Значит, возможно разместить 10 событий.
В бинарном пятиразрядном слове надо найти число всех составных событий длины 5. На пересечении столбца имеющего заголовок «5» (длина слова) и строки 5S (события длины 5) находится число 2 - возможно разместить два события.
Числа в таблице 6 рассчитываются по формуле расчёта составных событий в рядах: I(n) и L(n) – рёбер графа с рис.2:
![]() (11)
(11)
При n=1 (11) выдаёт 1S = 3/2 вместо необходимой в таблице 6 двойки. Но возможно, что одноразрядное слово (просто подбрасывание монеты) рассчитывается как сумма двух слагаемых, первое из которых (11), а второе 0S – нулевое составное событие, в котором N = n = 1:
![]() (11.1)
(11.1)
где N = n = 1.
Если (11.1) верна, то при подбрасывании монеты как жребия на выпадение её сторон действуют ещё не исследованные, виртуальные, составные события нулевой длины. Причём, как видно из (11.1) их процентное отношение равно 25%.
Таб. 6 можно сравнить с равнобедренной пирамидой, в основании которой лежит ряд из двоек. Затем ряд из четвёрок, из десяток. И т.д.
Обобщающие резюме по предсказанию событий
В статье показано на (7.1) и (7.2), что при конечных числах N, бросков монеты в потоковой последовательности, вероятность повторного выпадения текущего состояния монеты отличается на небольшую величину от вероятности не выпадения текущего состояния монеты. При большом количестве бросков вероятности выравниваются до привычных 0,5.
В статье [4] был описан эксперимент, в котором на основе анализа выпавших состояний монет удалось добиться предсказаний выпадений двух различных процессов, с разными процентными соотношениями составных событий. И, на данный момент, можно получать по желанию, на основе анализ событий выпавшей монеты, три потока монетных выпадений. Каждый из потоков обладает своей собственной процентной структурой составных событий. Процентные соотношения двух потоков описаны в работе [4]. Процентные соотношения (коэффициенты) по ф.1, описаны в работе [2].
Пока я разделяю мнение, что прошлые результаты выпадений монеты не влияют на её будущие результаты. Но в своих работах показываю, что возможно угадать некоторые параметры будущего случайного (р=0,5) процесса выпадения монеты, анализируя выпавшие его составные события. Разум (в философском смысле), программа, анализируя физический процесс выпадения монеты, накладывает через предсказания выпадений свой отпечаток на угаданные события. Программа, анализируя выпадающие события потоковой последовательности, принимает решения о том, будут ли делаться предсказания или нет [4]. Последовательность, составленная из выпадений монеты, формируемые программой до их выпадения, уже будут иметь другую структуру составных событий, чем структура составных событий исходной потоковой последовательности. Сейчас принято считать, что изменить структуру результатов выпадения монеты, на основе предсказаний её выпадений – невозможно. Но в работе [4] описан эксперимент и алгоритм, приводящие к изменению структур предсказываемых процессов выпадения монеты.
Литература
1. Филатов О. В., Филатов И.О., Макеева Л.Л. и др. «Потоковая теория: из сайта в книгу». М.: Век информации, 2014. С.200.
2. Филатов О. В., Филатов И.О., Статья «О закономерностях структуры бинарной последовательности», «Журнал научных публикаций аспирантов и докторантов», № 5, 2014.
3. Филатов О. В., Филатов И.О., Статья «О закономерностях структуры бинарной последовательности (продолжение)», «Журнал научных публикаций аспирантов и докторантов», № 6, 2014.
4. Филатов О. В., Филатов И.О., Статья «О закономерностях структуры бинарной последовательности (продолжение 2)», «Журнал научных публикаций аспирантов и докторантов», № 7, 2014.
5. Филатов О. В., Статья «Методика поиска степени родства языков по чередованию гласных и согласных букв в письменных источниках», «Журнал научных публикаций аспирантов и докторантов», № 9, 2014.
Поступила в редакцию 18.11.2014 г.