Актуарные расчеты страховых тарифов

Актуарные расчеты страховых тарифов

Дорофеев Борис Вячеславович,

кандидат физико-математических наук, доцент.

Санкт-Петербургский государственный университет.

Actuarial insurance rates

Boris Dorofeev,

PhD, Assistant Professor. Saint Petersburg State University.

Работа посвящена методике расчетов нетто-премий по договорам страхования жизни, в которой впервые вводится процентная ставка, как нормальная случайная величина. Получены параметры распределения вводимых случайных величин и на их основе вычисляются тарифы договоров страхования жизни.

Ключевые слова: страхование жизни, аннуитет, актуарные расчеты.

Article is devoted to methods of calculation of net premiums on life insurance policies, which first introduced the interest rate as a normal random variable. Parameters of the distribution of entered random variables and their rates are calculated based on life insurance contracts.

Keywords: life insurance, annuity, actuarial calculations.

Введение

Актуарные расчеты в страховании – это расчет тарифных ставок в страховании жизни. Они производятся на основе методологии актуарной оценки рисков и вероятностей наступления страховых случаев. Основными факторами, влияющими на методику расчета тарифных ставок по страхованию жизни, являются следующие:

1. Объектом договора страхования является трудоспособность клиента, его здоровье и сама жизнь. Страховой случай – это потеря одного из указанных атрибутов. Количественные показатели, характеризующие продолжительность жизни и вероятность возникновения болезней, учитываемых в договоре, собираются в федеральных и региональных органах статистики и обрабатываются в страховых компаниях. На основании демографической статистики составляются таблицы смертности и аналитические законы демографии. Именно эти данные используются актуариями при расчете тарифных ставок. Продолжительность жизни отдельного человека имеет случайный характер, поэтому при ее оценке используются методы математической теории вероятностей и статистики.

2. Договоры страхования жизни заключаются, как правило, на длительный срок, то есть период времени между уплатой страховой премии и моментами выплат проходит нескольких лет, и они могут длиться до смерти застрахованного лица. В этот период деньги находятся в страховом фонде и его стоимость меняется в зависимости от инфляции и прибыли, получаемой в результате инвестирования. Данный фактор учитывается при расчете тарифных ставок в форме дисконтирования платежей. В настоящей работе предполагается рассмотреть силу роста процента изменения страхового фонда как случайную величину. Будем считать, что в различные периоды времени эта случайная величина различна, но имеет один закон распределения. Самой распространенной и изученной является нормальная случайная величина. Если мало что известно о поведении случайной величины, то обычно при моделировании ее принимают нормально распределенной, так как она обладает замечательными свойствами. В том числе, согласно центральной предельной теореме, сумма одинаково распределенных случайных величин стремится к нормальной.

Страхователь выплачивает страховщику за его услугу страховую премию. Эта брутто-премия состоит из нетто-премии, которая формирует страховой фонд, и нагрузки. Нагрузка служит для покрытия расходов и формирования прибыли страховщика. Нетто-ставка отражает меру риска и представляет главный интерес актуария. Предлагается построить методику расчетов нетто-премий, как точечных и доверительных оценок. Указанные оценки получаются при анализе баланса в модели финансовых потоков, обусловленных случайным характером смерти застрахованного лица и случайной силой роста процента при инвестировании страхового фонда.

Постановка задачи

В рамках предположений, описанных выше, обозначим через – целочисленную случайную величину продолжительность предстоящей жизни лица, дожившего до возраста х лет. Ее распределение можно записать в следующем виде

, ,

где – предельный возраст жизни (100 – 110 лет для различных таблиц смертности). Вероятность прожить еще лет лицу в возрасте лет определяется из таблицы смертности, которой пользуется актуарий страховой компании.

Из свойств вероятности

где – вероятность прожить n лет для лица, прожившего лет.

, ,

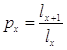величины – число лиц, доживших до лет из некоторой замкнутой совокупности людей (обычно 100 000 человек), заданы в таблице смертности.

Требуется определить нетто-премию ежегодных равных платежей до наступления страхового случая (смерти), исходя из принципа эквивалентности финансовых потоков, приведенных к одному моменту времени.

Описание предлагаемого подхода

Обычно в актуарных расчетах процентная ставка роста страхового фонда принимается детерминированной. Сила роста процента определяется из соотношения , а коэффициент дисконтирования .

Поток единичных ежегодных платежей в течение n лет приведенный к настоящему времени называется современной стоимостью или аннуитетом

Современная стоимость бессрочной ренты – случайная величина. Ее математическое ожидание

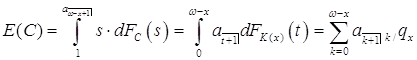Подставляя значения срочного аннуитета и вероятностей, получим точечную оценку нетто-тарифа: 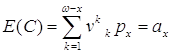. Более адекватной является доверительная оценка , где надбавка с большой вероятностью гарантирует, что страхового фонда из аналогичных договоров хватит для исполнения обязательств по выплате ренты. Величина находится из условия и равна , где – квантиль с уровнем доверия .

Для вычисления доверительной оценки необходимо вычислить дисперсию случайной величины (Кудрявцев А.А.):

. (1)

Данная работа посвящена методике получения оценок нетто-премии в условиях предположения о нормальном распределении силы роста процента. Будем считать, что на -ом периоде времени сила процента случайная величина

где – параметры распределения. Известно, что . Тогда на каждом периоде времени свой коэффициент дисконтирования .

Современная стоимость потока единичных платежей будет рассчитываться по формуле

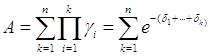Обозначим через . Эта случайная величина тоже имеет нормальное распределение .

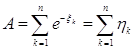Введем еще одну случайную величину , , тогда величина преобразуется . В общем случае стоимость бессрочного аннуитета есть случайная величина 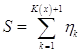, зависящая от случайной величины и набора случайных величин .

В качестве оценок нетто-премии найдем точечную и доверительную оценку величины

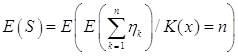
– условное математическое ожидание.

Рассмотрим

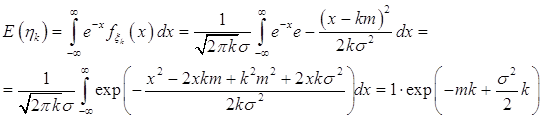
Обозначим через , тогда . Благодаря получившейся формуле математического ожидания следует, что 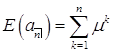. Значит

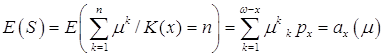. (2)

Модель, включающая предположение о нормальном распределении силы процента имеет смысл, если выполняется , то есть параметры и таковы, что или . Для доверительной оценки необходимо найти дисперсию случайной величины S

Первое слагаемое найдем по формуле условного математического ожидания

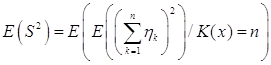. (3)

Рассмотрим

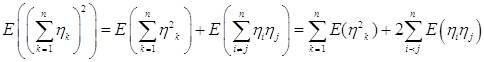Исследуем каждое слагаемое:

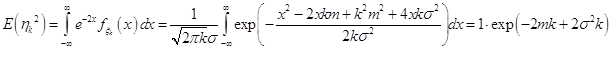Если обозначить , то .

Будем предполагать, что случайные величины попарно независимы, то есть для . Величины и зависимы. Тогда

В результате получаем

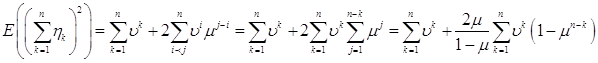Приведем подобные слагаемые, вынесем в третьем слагаемом за знак суммы множитель и обозначим через , получим

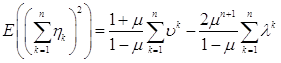Возвращаемся к формуле (3)

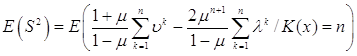Аналогично преобразованиям формулы (2), подставляем

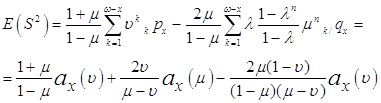
Тогда окончательно

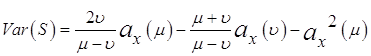Заметим, что дисперсия величина положительная, следовательно, должно выполняться неравенство , отсюда , значит . Получаем ограничение на параметры распределения .

Заключение

В данной работе решена задача построения алгоритма вычисления нетто-премий в договорах бессрочного страхования жизни в условиях случайной силы процента. Предлагаемый подход позволяет вычислять и иные тарифы в различных договорах страхования жизни, используя известные соотношения. Заметим, что в предельном случае, когда дисперсия случайной величины стремится к нулю, сама величина становится детерминированной, равной своему математическому ожиданию. Полученные формулы нетто-премий полностью согласуются с известными актуарными соотношениями, то есть если в них положить , то формулы математического ожидания и дисперсии нетто-тарифов совпадут.

Литература

1. Кудрявцев А.А. Актуарная математика: Оценка обязательств компании страхования жизни. Учебное пособие. – 2-е изд.– СПб.: Изд-во С.-Петерб. ун-та, 2005. – 240 с.

Поступила в редакцию 23.01.2014 г.