О функциях мощности контрольных карт асимметрии и эксцесса нормального процесса

Ахмедов Сахибджан Акбарович,

кандидат физико-математических наук, доцент,

Андижанский государственный университет,

Эгамбердиева Барнахан Гулямджановна,

Захидов Дилшодбек Гулямджанович,

Аблазова Камола,

ассистенты.

Андижанский сельскохозяйственный институт.

Пусть распределение измеримого признака качества Х в генеральной совокупности имеет нормальное распределение -  выборка взята из Х,

оценки  соответственно.

Обозначим через

соответственно выборочные коэффициенты асимметрии и эксцесса .  и  квантили статистик  и  при заданном уровне значимости .

Известно, что на практике важным является стабильность или воспроизводимость изучаемого процесса. Стабильность процесса зависит от обычных (случайных) и особых (неслучайных) причин. Эти причины сильно влияют на распределение изучаемого процесса Х. Распределения могут различаться по положению, разбросу и форме. Разброс и форму можно проверить при помощи статистик  и . Если имеют место только обычные причины вариаций, то результаты процесса образуют распределение, которое является стабильным во времени и предсказуемым. Если имеют место особые причины вариаций, то результат процесса не является стабильным во времени.

Если установлено, что процесс стабилен и способен соответствовать требованиям в данный момент, следует выполнить дополнительные исследования. При этом, если собрано достаточное количество данных то они строятся на контрольной карте (КК) и если не найдены особые причины, то могут быть вычислены долговременные показатели воспроизводимости и настроенность процесса [1].

В контроле производства для оценких КК используется функция мощности критерия

,

где  - тестовая величина (критерий),  - область отклонения гипотезы,  - значение неизвестного параметра распределения . При помощи  проверяются следующие сложные гипотезы:

 является нормальной;

 не является нормальной.

В [2] для повторной проверки гипотез было предложено КК асимметрии и эксцесса:

Утверждение 1:

КК асимметрии с односторонней границей имеет вид:

где НКГ (нижняя контрольная граница) определяется следующим образом:

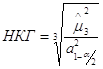
- значение в текущий момент времени t, - усредненное значение совокупности величин

значение  для некоторых  и находим из [3].

Утверждение 2:

КК эксцесса с двусторонними границами имеет вид:

Здесь НКГ и ВКГ (верхняя контрольная граница) определяются следующим образом:

,

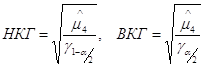где - усредненное значение совокупности величин

значение  и  для некоторых  и находим из [3].

В данной работе мы приводим оценки КК асимметрии и эксцесса. При этом текущее стандартное отклонение процесса.

Утверждение 3:

При условиях утверждений 1 и 2 функция мощности КК асимметрии  и эксцесса  соответсвенно имеют следующий вид:

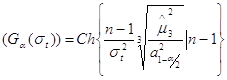
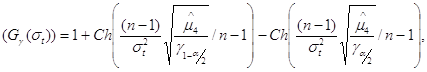
Здесь обозначено через  распределение с  степенью свободы.

Литература

1.                  Х.Й.Миттаг, Х.Ринне. Статистические методы обеспечения качества. – М.: Машиностроение, 1995.

2.                  С.А.Ахмедов. Контрольные карты асимметрии и эксцесса нормального процесса. Материалы республиканской научно-практической конференции. Статистика и её применения. Ташкент, 2012, с.279-280.

3.                  Л.Н.Большев, Н.С.Смирнов. Таблицы математической статистики. – М.: Наука, 1983.

Поступила в редакцию 17.03.2014 г.