Формирование оптимального портфеля активов, моделируемых стохастическими дифференциальными уравнениями Ито
Микишанина Евгения Арифжановна,
старший преподаватель Чувашского государственного университета им. И. Н. Ульянова.
Задача формирования оптимального портфеля ценных бумаг (активов), цены которых моделируются случайными процессами, является одной из актуальных проблем современной финансовой математики. При составлении такого портфеля инвестор сталкивается с необходимостью оценки ожидаемой доходности каждого актива и связанного с ним риска неполучения дохода. Очень часто активы рассматриваются в конкретный момент времени и сроятся предположения на основе теоретико-вероятностной трактовки выше упомянутых понятий. Однако стоимость ценных бумаг можно рассматривать и как случайный процесс на некотором промежутке времени со своими числовыми характеристиками, такими как математическое ожидание и дисперсия.
Пусть ![]() - капитал инвестора в момент времени
- капитал инвестора в момент времени ![]() . Предположим, что он инвестирует свои
средства в
. Предположим, что он инвестирует свои
средства в ![]() различных рисковых активов. Будем
считать, что цены каждого актива
различных рисковых активов. Будем
считать, что цены каждого актива ![]() являются решением
стохастических дифференциальных уравнений Ито
являются решением
стохастических дифференциальных уравнений Ито
![]() ,
,
где ![]() - постоянные, которые характеризуют
мгновенное изменение трендовой составляющей и степень будущей изменчивости цены
актива (волатильность),
- постоянные, которые характеризуют
мгновенное изменение трендовой составляющей и степень будущей изменчивости цены
актива (волатильность), ![]() - независимые
стандартные винеровские процессы,
- независимые
стандартные винеровские процессы, ![]() В начальный момент
времени капитал является детерминированной величиной, равной
В начальный момент
времени капитал является детерминированной величиной, равной ![]() .
.
Инвестор
распределяет свой капитал между данными активами в долях ![]() соответственно, причем
соответственно, причем ![]() ,
, ![]() . Тогда
стохастическое дифференциальное уравнение для капитала примет вид
. Тогда
стохастическое дифференциальное уравнение для капитала примет вид
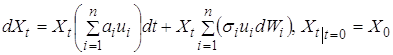 .
.
Закон изменения величины капитала во времени будет иметь вид
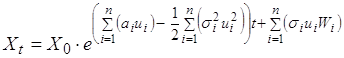 . (1)
. (1)
Математическое ожидание случайного процесса (1) примет вид
![]() (2)
(2)
дисперсия -
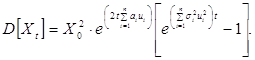 (3)
(3)Математическое ожидание (2) и дисперсия (3) являются функциями 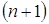 -й неизвестной
-й неизвестной 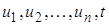 .
.
Одна из целей, которую преследует инвестор, – это минимизация дисперсии величины капитала как случайного процесса и максимизация ожидаемой выгоды от капитала в последующие моменты времени. Одновременно это сделать невозможно. Но можно зафиксировать желаемый уровень будущей ожидаемой величины капитала и при этих условиях минимизировать дисперсию. Эта задача известна как первая задача Марковица, [1].
В нашем случае эта задача примет вид:(4)
где 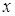 - константа, определяющая ожидаемую инвестором величину капитала.
- константа, определяющая ожидаемую инвестором величину капитала.
Получить желаемую
величину капитала можно в любой момент из некоторого временного интервала,
который определяется ограничениями системы (4). Более того, инвестируя все средства
в актив с наибольшей составляющей ![]() , желаемый уровень капитала
, желаемый уровень капитала ![]() можно достичь максимально быстро. Но,
как правило, активы с большей ожидаемой доходностью, а, соответственно, и с
большей скоростью изменения трендовой составляющей
можно достичь максимально быстро. Но,
как правило, активы с большей ожидаемой доходностью, а, соответственно, и с
большей скоростью изменения трендовой составляющей ![]() , обладают и большей волатильностью. Поэтому и
дисперсия такого портфеля будет достаточно велика. Решение задачи (4) поиска
условного экстремума позволяет определить момент времени, к которому будет
достигнут желаемый уровень величины капитала при минимальной дисперсии, а также
доли вложений в имеющиеся активы.
, обладают и большей волатильностью. Поэтому и
дисперсия такого портфеля будет достаточно велика. Решение задачи (4) поиска
условного экстремума позволяет определить момент времени, к которому будет
достигнут желаемый уровень величины капитала при минимальной дисперсии, а также
доли вложений в имеющиеся активы.
Задача (4) для конкретных данных может быть решена разными способами, например, методом множителей Лагранжа с ограничениями типа равенств и неравенств, методом исключения некоторых неизвестных, численными методами. Однако, в общем виде для произвольного количества активов эту задачу решить довольно сложно.
Решим в общем виде задачу для двух рисковых активов. В этом случае система (4) примет вид
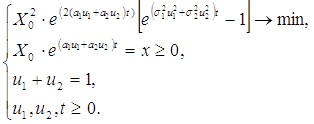 (5)
(5)
Пусть 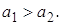 Сделаем замену
Сделаем замену.
Целевая функция системы (5) примет вид. (6)
Находя экстремум функции (6) и, учитывая, что 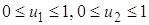 , получим:
, получим: 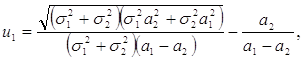 (7)
(7)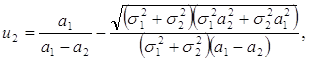 (8)
(8)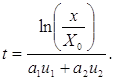 (9)
(9)
Итак, для портфеля, состоящего их двух рисковых ценных бумаг, определены доли активов в портфеле (7),(8) и момент времени (9), к которому будет достигнут желаемый уровень капитала, при этом дисперсия капитала как случайного процесса будет минимальна.
Литература
1. Уильям Ф. Шарп. Инвестиции / Уильям Ф. Шарп, Гордон Дж. Александер, Джеффри В. Бейли. - М.: ИНФРА-М, 1999. – 1028с.
Поступила в редакцию 20.07.2015 г.