Теплофизические свойства соединения CuGa₂InTe₅

Гасанова Мехрибан Ширин кызы,

кандидат физико-математических наук, доцент, докторант Азербайджанского технического университета, г. Баку.

Исследованы температурные зависимости удельной электропроводности, коэффициента термо-э.д.с., общей теплопроводности, холловской подвижности носителей зарядов, коэффициента продельного эффекта Нернста-Эттингаузена, маг­нитного сопротивления и магнитотермо.-э.д.с. нового соединения CuGa₂InTe₅. Выявлены механизмы рассеяния электронов и фононов в кристаллах этого соединения.

Ключевые слова: монокристалл, полупроводниковое соединение, электрон-фононное рассеяние.

При исследовании характера физико-химического взаимодействия между In₂Te₃~ Cu₂Ga₄Te₇ при соотношении исходных компонентов 1:1 нами обнаружено новое соединение CuGa₂InTe₅ с конгруэнтным плавлением при ~1028 К. При рентгенографическом анализе определено, что рентгенограмма этого соединения незначительно отличается от рентгенограммы известного по литературе [1] соединения CuGa_1,8In_1,2Te₅, кристаллизующегося в тетра­гональ­ной структуре параметрами а=6,043и с=12,068. В данном сооб­щении приводятся результаты температурных зависимостей удельной элек­тропроводности (s), коэффициента термо-э.д.с. (a), общей тепло­проводности (æ_общ), холловской подвижности носителей заряда (U_х), а также некоторых термомагнитных (продольный коэффициент Нернста-Эттин­гаузена e_у, магнитосопротивление  и магнитотермо-э.д.с. ) коэф­фициентов. Одновременно, используя данные температурной зависи­мости обшей теплопроводности, рассчитаны и построены температурные зави­симости фононного термосопротивления и биполярной теплопроводности.

Измерения теплофизических параметров проводили на монокристалл­лических образцах параллелепипедной формы по методике [2], в интервале температуры 300-850 К. Монокристаллы получали методом направленной кристаллизации на установке Бриджмена-Стокбаргера.

На рис. 1 приведена температурная зависимость удельной электропро­водности (s) и коэффициента термо.-э.д.с. (a) соединения CuGa₂InTe₅. Ход кривой зависимости  полуметаллический.

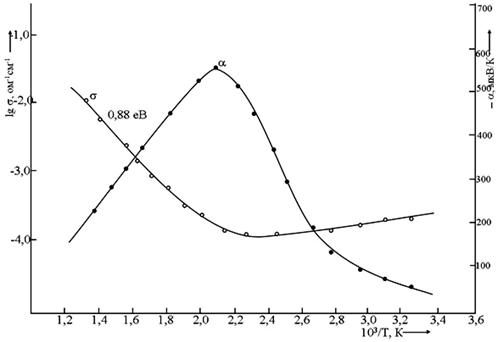
Рис. 1. Температурная зависимость удельной электропроводности (s) и коэффициента термо-э.д.с. (a) соединения CuGa₂InTe₅.

Начиная с~413К наблюдается заметный рост электропроводности, что, по-видимому, связано с приближением собственной области проводимости. Согласно наклону кри­вой в этой области рассчитано значение термической ширины запрещенной зоны (DЕ_терм=0,88 эВ). Коэффициент термо-э.д.с. вначале прямолинейно растет, проходя через максимум, затем начинается её сильное уменьшение. Прямолинейный рост коэффициента термо-э.д.с. до определенной темпе­ратуры присущ полупроводникам со сложной зонной структурой [3], у которых при низких температурах зависимости a_экс(Т) качественно согласуются с зависимостями a_теор(Т), рассчитанными при предположении постоянства концентрации и эффективной массы носителей заряда, а также фактора рассеяния «r», которым равней нулю. Выше температуры ~473 наблюдается сильное уменьшение коэффициента термо-э.д.с., связанное с одной стороны наступлением собственной области проводимости, а с другой – ростом степени вырождения носителей заряда. Во всем исследованном температурном интервале коэффициент термо-э.д.с. обладает отрицательным знаком проводимости .

Рисунок 2 отражает температурную зависимость холловской подвиж­ности (U_х) коэффициента продельного эффекта Нернста-Эттингаузена (e_у) соединения CuGa₂InTe₅.

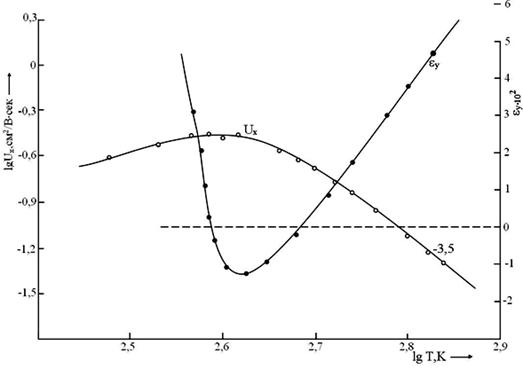
Рис. 2. Температурная зависимость холловской подвижности носителей заряда (U_х) и коэффициента продольного эффекта Нернста-Эттингаузена (e_у) соединения CuGa₂InTe₅.

Установлено, что до температуры ~400К изменение холловской под­виж­ности носителей заряда подчиняется закону ~Т^1,5, что соответствует рассеянию электронов от ионизированных примесных центров. Проходя через пологий максимум, при высоких температурах, наблюдается умень­шение подвижности согласно закону ~Т^-3,5. Это свидетельствует о рассеянии носителей зарядов от тепловых колебаний кристаллической решетки. Изменение механизма рассеяния электронов в исследуемом соединении под­тверждается и температурной зависимостью коэффициента продольного эффекта Нернста-Эттингаузена (рис. 2, кривая e_у), который претерпевает инверсию знака в зависимости от температуры. Пологий максимум на зависимости lg(U_x) ~ f(lgT) свидетельствует о присутствии еще одного меха­низма рассеяния носителей заряда в исследуемых кристаллах. Это – рассеяние носителей от полярных оптических колебаний кристаллической решетки.

Температурная зависимость общей теплопроводности соединения CuGa₂InTe₅ приведена на рис. 3.

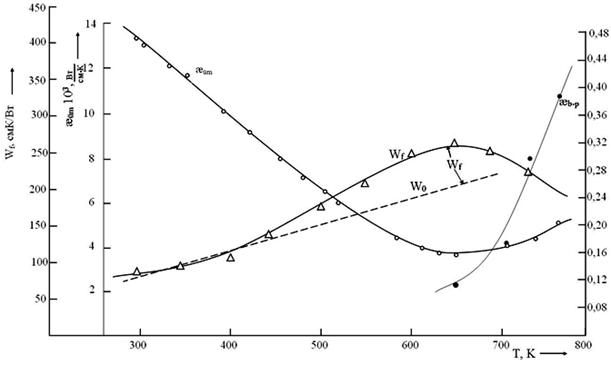
Рис. 3. Температурная зависимость общей теплопроводности (æ_общ), теплосопротивления кристаллической решетки (W_f) и биполярной теплопроводности (æ_б-п) соединения CuGa₂InTe₅.

Как видно, начиная от комнатных темпера­тур до ~650К, общая теплопроводность подчиняется отрицательному степен­ному закону, что свидетельствует о нормальных фононных процессах, происходящих в исследуемом кристалле. Однако, выше 650К общая тепло­проводность проявляет тенденцию к увеличению. Для разъяснения меха­низма, теплопереноса были рассчитаны электронные, фононные и биполяр­ные доли общей теплопроводности. Электронная теплопроводность рас­счи­тана согласно закону Видемана-Франца [4], согласно которому æ_эл=LsT, где: L – число Лоренца (для невырожденных полупроводников L=2,4×10^-8, s – удельная электро­проводность, а Т – температура. Зная значение æ_эл., затем по формуле æ_ф=æ_общ – æ_эл найдены значения фононной теплопроводности, а её обратное значение представило данные для теплосоп­ро­тивления кристал­лической решетки. Пренебрегая вкладом теплопро­вод­ности дефектов, так как считается, что в монокристаллах число дефектов ничтожно мало.

На рис. 3. также представлена температурная зависимость теплосопро­тив­ления кристаллической решетки (W_f). До температуры ~423К фононное теплосопротивление по температуре изменяется аналогично теоретическому значению этого параметра (W₀). Однако, начиная от температуры ~450К в кристалле CuGa₂InTe₅ появляется дополнительное фононное тепло­соп­ро­тив­ление DW_f, вследствие которой, рассеяние фононов происходит от дефектов кристалл­лической решетки. Количественно дополнительное фононное тепло­вое сопротивление можно оценить как DW_f = W_f – W_{­трехфонон}. По темпера­тур­ной зависимости фононного теплосопротивления найдено, что тепло­про­водность соединения CuGa₂InTe₅ подчиняется закону ~ Т^-0,32. Это свиде­тельствует о наличии трехфононного механизма рассеяния в исследуемом кристалле. Как видно из температурной зависимости общей теплопро­вод­ности (рис. 3) такой механизма может продолжатся до ~653 К, так как начи­ная от этой температуры, наблюдается рост общей теплопроводности. Обычно подобный рост æ_общ при высоких температурах может быть объяснен вкладом биполярной составляющей теплопровод­нос­ти. Учитывая это по фор­муле æ_б-п=2LsТ приведенной в [5] вычис­ле­ны значения биполярной сос­тавляющей теплопроводности. Температурная зависимость этого пара­метра приведена на рис. 3. Как видно, при высоких температурах æ_б-п сильно раст­ет, от чего и можно считать, что её вклад в общую теплопроводность заметный.

На рис. 4 приведены температурные зависимости магнитосопротивления  и магнитотермо-э.д.с.  соединения CuGa₂InTe₅. Как видно, у обоих параметров наблюдается инверсия знака, что свидетельствует об сме­щенном механизме переноса электронов и фононов в кристалле CuGa₂InTe₅. Отрицательный знак  указывает, также на малую подвиж­ность носителей заряда в исследуемом материале.

Таким образом, исследование температурных зависимостей кинети­чес­ких коэффициентов в CuGa₂InTe₅ указывает на смешанный механизм пере­но­са носителей заряда и тепла, связанных, по-видимому, с многокомпонент­ностью состава и сложностью зонной структуры.

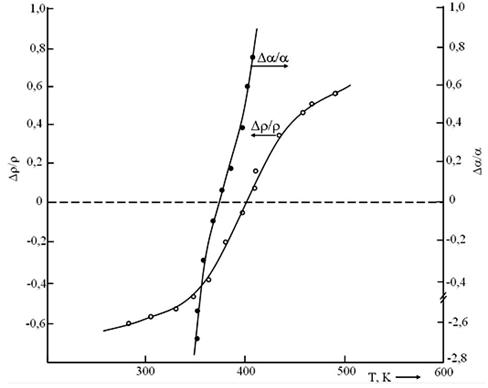
Рис. 4. Температурная зависимость магнитосопротивления  и магнитотермо-э.д.с.  соединения CuGa₂InTe₅.

Литература

1.                  Guevara R., Dekgodo F., Wasim S., Rinco C., Sanchez Perez G. X-ray power dif­fraction, phase transitions and optical characterization of the Cu(In_1-xGa_x)₃Te₅ semiconducting system // F.Alloys Compds. 2005, Vol 393, p. 100.

2.                  Крегова М.А., Авилов Е.С., Земсков В.С. Введение в методику экспериментов. Результаты и их обсуждение. М., Наука, 2004, 196 с.

3.                  Rogers I.M. Valence band structure of PbTe // Brit. J.Appl. Phys. Ser.2, 1968. Vol. 1, N7, p. 845

4.                  Могилевский Б.М., Чудновский А.Ф. Теплопроводность полупровод­ников. М., Наука, 1972, 536 с.

5.                  Охотин А.С., Боровикова Р.П., Нечаева Т.В., Пушкарский А.С. Тепло­про­водность твердых тел (Справочник). М., Энергоатомиздат, 1984, 320 с.

Поступила в редакцию 05.02.2015 г.