Некоторые следствия фундаментального характера, вытекающие из анализа теории относительности

 

Мигунов-Миллер Сергей Николаевич.

 

В статье показано, что можно с иной, чем в Специальной теории относительности, точки зрения объяснить физические явления, которые приведены Эйнштейном в своей работе «К электродинамике движущихся тел». Рассмотрена одна из основных причин, приведших к созданию Эйнштейном неверных теоретических разработок. Проанализировано положение о физической эквивалентности системы отсчёта, связанной с гравитационным полем и равномерно ускоренно движущейся системой отсчёта. Показана их физическая неравноценность. Соответственно этому высказана сомнительность в научной объективности основы, на которой построена Общая теория относительности.

 Ключевые слова: Специальная теория относительности, эффект Доплера, системы отсчёта, Общая теория относительности, гравитационное поле, равномерно ускоренная система отсчёта, эквивалентность систем отсчёта.

 

В предыдущей нашей работе [1, с.125-139] аналитически была показана ошибочность положений основополагающей статьи Специальной теории относительности « К электродинамике движущихся тел». Однако, наряду с основными результатами проведённых исследований, показывающих несостоятельность Специальной теории относительности, некоторые выводы из анализа требуют определённых пояснений. Кроме того, и это самое главное, остаётся открытым вопрос о соответствии физическим реалиям положений Общей теории относительности, и тем самым всей теории относительности в целом.

Ранее нами было высказано утверждение о том, что движущиеся в пространстве тела действительно испытывают в направлении своего движения продольные сокращения линейных размеров. Величина этих сокращений определяется соотношением β = (1−v²/c²)^1/2. Однако эти сокращения, в отличие от положений Специальной теории относительности, носят причинно-следственный характер. Другими словами эти сокращения присущи тому или иными движущемуся физическому телу, представляющему собой совокупность тех или иных частей, из которых это тело состоит, и тем или иным образом взаимодействующих между собой. Эти сокращения обусловлены нахождением движущегося тела в целом и частей его составляющих в состоянии статического равновесия. Подобная точка зрения не нова. Так, к примеру, ещё в 1921 году в своей работе «Теория относительности» Вольфганг Паули писал [2, с.14]:

«…Лоренц … и независимо от него Фитцжеральд предположили, что все тела, движущиеся поступательно со скоростью v, изменяют свои размеры. Именно, было предположено, что в направлении движения уменьшение размера тела определяется множителем  , где ϰ – изменение размеров в направлении, перпендикулярном к скорости тела; само ϰ остаётся неопределённым. В целях обоснования этой гипотезы Лоренц указывал на возможность изменения молекулярных сил при поступательном движении. Действительно, если предположить, что молекулы находятся в положениях равновесия, а силы взаимодействия между ними носят чисто электростатический характер, то из теории непосредственно следует, что в движущейся системе равновесие наступит тогда, когда все расстояния между частицами в направлении движения сократятся в отношении , а расстояния в направлениях, перпендикулярных к скорости тела, останутся неизменными».

Наша позиция отличается от только что приведённой тем, что в дополнение к мнению В. Паули, коэффициент ϰ в указанном множителе, несмотря на кажущуюся неопределённость, соответствует размерам тела в направлениях, перпендикулярных к его скорости при любом значении последней, т.е. в интервале 0 < v < c. Следовательно, в этом смысле, ϰ = const.

В согласии с нашей точкой зрения приведённое выше предположение находится в неразрывном единстве с выполнением положений об изотропности пространства, о безусловной причинно-следственной зависимости протекающих процессов и об инвариантности скорости распространения света. Далее, из безусловного выполнения положения о постоянстве скорости распространения света в пространстве, следует явление замедления протекания всех процессов в движущейся со скоростью v физической системе в отношении .

Необходимо отметить, что в полном соответствии приведённой позиции, однозначно можно заключить: скорость v движения тела в указанном множителе есть абсолютная скорость движения тела в пространстве. В отличие от позиции последователей теории относительности, для которых указанная скорость является относительной. При такой нашей трактовке рассматриваемого явления полностью объясняется, как мы указывали ранее, так называемый «парадокс близнецов».

Исходя из всего только что сказанного, как пример, рассмотрим любое из физических явлений, которое объясняется в известной статье «К электродинамике движущихся тел» посредством преобразований СТО, но основываясь на наше виденье их разрешения. А затем проанализируем полученные результаты.

Обратимся к §7 упомянутой статьи «Теория аберрации и эффекта Доплера». Рассмотрим здесь эффект Доплера.

Акустический эффект Доплера обусловлен относительным движением источника и приемника акустических волн и выражается формулой

ν=ν₀(1 ± u/v)                                                                                                            (1)

где, ν – наблюдаемая частота акустических волн; ν₀ – частота источника волн; v – скорость волн относительно несущей среды; u – величина относительной скорости сближения или удаления наблюдателя и источника акустических волн.

Формула справедлива при выполнении условия

u_н / v << 1, u_u / v << 1                                                                                              (2)

где u_н – величина скорости наблюдателя относительно среды; u_u – величина скорости источника относительно среды.

При этом u = u_н + u_u

Полная формула, выражающая акустический эффект Доплера имеет вид

ν=ν₀(v±u_н)/(v±u_u)                                                                                                     (3)

Само понятие «акустический» эффект говорит о наличии несущей среды, в которой распространяются волны. Согласно нашим представлениям электромагнитные волны есть колебания материи, которая и является несущей средой. Подробнее это будет рассмотрено впоследствии, но то, что это так, вне всякого сомнения. В этой связи естественно предположить, что эффект Доплера для электромагнитных волн должен выполняться, что и подтверждается экспериментально.

Рассмотрим наличие эффекта Доплера для электромагнитных волн с нашей, новой точки зрения.

Пусть имеется источник монохроматических волн с частотой колебаний ν₀ и наблюдатель, находящийся на расстоянии r₀ от источника в некоторый произвольный момент времени, который примем за начало отсчета, т.е. в момент t₀ = 0.

Пусть скорость движения источника в пространстве будет равна v и угол между линией наблюдения (т.е. линией, соединяющей наблюдателя и источник) и вектором скорости источника в начальный момент времени будет равен β₀ (рис.1).

Уравнение световой волны, испускаемой источником по направлению к наблюдателю, как известно, имеет вид

E,H=Acos[w/(t–r/c)+a]                                                                                            (4)

Здесь w – частота, с которой колеблется источник; а ─ начальная фаза колебаний источника.

Сам источник в это же самое время движется по своей траектории с постоянной скоростью v. Следующее за первоначальным, такое же значение поля при колебании электрических диполей источника будет по прошествии некоторого промежутка времени, равного периоду колебаний Т₀. Источник при этом сместится от первоначального положения на расстояние S₀S_t, равное

S₀S_t=v∙T₀                                                                                                                                                        (5)

Точку наблюдения первый фронт волны достигнет через промежуток времени, равный

Δt₁=r₀/c                                                                                                                     (6)

Второй фронт с таким же значением поля достигнет наблюдателя через промежуток времени (относительно второго положения источника)

Δt₂=r₁/c                                                                                                                     (7)

где r₁ – расстояние от источника до наблюдателя во втором его положении, в котором значения составляющих поля точно такие же, как и в начальном положении, т.е. при t₀=0.

Очевидно, с учетом времени движения источника из первоначального положения во второе, период колебаний, воспринимаемый наблюдателем в точке наблюдения, будет определяться как

Т=Δt₂+Т₀–Δt₁                                                                                                           (8)

Или иначе, с учетом (6) и (7)

Т=Т₀+(r₁–r₀)/c                                                                                                           (9)

Отложим от точки наблюдения 0 (рис. 1) на прямой, соединяющей эту точку наблюдения и второе положение источника отрезок, равный r₀ и соединим полученную точку К с точкой S₀, т.е. с положением источника в первоначальный момент времени. Тогда согласно рис.1 можно заключить, что

Т=Т₀+(r₀+r_g–r₀)/c=Т₀+r_g/c                                                                                         (10)

 

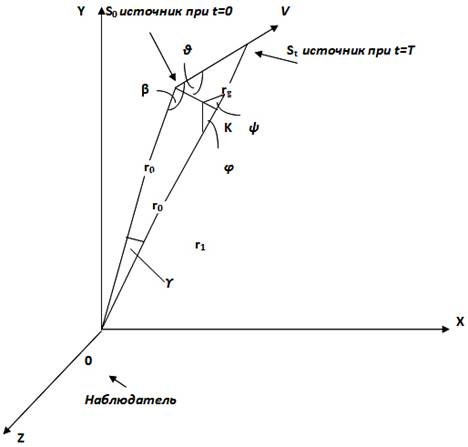
Рис.1

 

Здесь обозначено: ОS₀ = OK = r₀; KS_t = r_g.

Отметим, что Т₀ – собственный период колебаний диполей источника в покое. При движении источника со скоростью v, согласно нашим представлениям, все процессы в движущемся источнике протекают медленнее по соответствующему закону, и поэтому (10) примет вид

T=T_V+r_g/c=(T₀ / ) + r_g /c                                                                       (11)

Определим расстояние r_g. Из треугольника S₀KS_t согласно теореме синусов

v∙T_V/sinψ=r_g/sinυ                                                                                                      (12)

Откуда

r_g=v∙T_Vsinυ/sinψ                                                                                                       (13)

В (12) и (13) T_V – то же самое, что и в (11)

Тогда

r_g=v∙T₀sinυ/∙sinψ                                                                                  (14)

и (11) примет вид

Т=(T₀/)(1+v∙sinυ/с∙sinψ)                                                                      (15)

Согласно рис.1, имеем

υ=β₀–π/2+γ/2, ψ = π/2 + γ/2                                                                                     (16)

В соответствии с этим (15) примет вид

T=(T₀ / ) [1 + v∙ sin (β₀ – π/2 + γ/2) / c ∙ sin(π/2 + γ/2)]

Т=(T₀ / ) {1+(v/c)∙[sinβ₀∙cos (π/2−γ/2)−cos β₀∙sin(π/2−γ/2)] / sin(π/2+γ/2)}

Т=(T₀ / ) {1 + (v/c)∙[(sinβ₀∙sin γ/2 − cos β₀∙cos γ/2)] / cos γ/2}

Т=(T₀ / ) [1 + (v/c) ∙ (sinβ₀∙tg γ/2 − cos β₀)]

Так как Т = 1 / ν, где ν – частота колебаний, то, переходя к частоте колебаний, получим

1 / ν = (1 / ν₀ ∙ ) [1 + (v/c) (sinβ₀∙tg γ/2 − cos β₀)].

Тогда

ν=(ν₀∙ )/[1+(v/c)(sinβ₀∙tgγ/2− cos β₀)]                                                  (17)

Исследуем полученную формулу. При β₀ = 0, то есть тогда, когда вектор скорости движения источника света лежит на прямой, соединяющей точку наблюдения и источник, и направлен от источника к наблюдателю

cos β₀ = 1; sinβ₀ = 0.

Отсюда

ν=ν₀()/[1 − (v/c)] = ν₀ [(1+v/c)/(1−v/c)]^1/2                                            (18)

и, следовательно, частота источника света в этом случае в точке наблюдения будет увеличиваться по отношению к собственной частоте.

При β₀=π, то есть тогда, когда вектор скорости движения источника света лежит на прямой, соединяющей точку наблюдения и источник, и направлен от наблюдателя и от источника, следует:

cos β₀ = −1; sinβ₀ = 0.

Тогда

ν=ν₀∙()/[1 + (v/c)] = ν₀ [(1−v/c)/(1+v/c)]^1/2                                           (19)

и, следовательно, частота источника света в этом случае в точке наблюдения будет уменьшаться по отношению к собственной частоте.

В случае, если v<<с, формулу (18) можно приближенно записать следующим образом:

ν≈ν₀[1+(1/2)(v/c)]/[1–(1/2)(v/c)]≈ν₀{[1 + (1/2)(v/c)]·[1+(1/2)(v/c)]}                       (20)

Отсюда, ограничившись членами порядка [v/c] ², получим

ν=ν₀(1+v/c)                                                                                                               (21)

Соответственно для формулы (19) будем иметь

ν≈ν₀[1–(1/2)(v/c)]/[1 + (1/2)(v/c)]≈ν₀{[1–(1/2) (v/с)]·[1–(1/2) (v/с)]},                     (22)

или ограничиваясь членами порядка [v/c]², получим

ν=ν₀(1−v/c)                                                                                                               (23)

Объединив формулы (21) и (23), получим

ν=ν₀(1±v/c)                                                                                                               (24)

Применяя точно такие же рассуждения и в тех случаях, когда покоится источник света, а движется наблюдатель, а также при одновременном движении, как источника, так и приемника света, придём к одинаковому результату. Необходимо только при этом помнить, что у движущегося наблюдателя все процессы протекают в β = (1 – v²/c²)^1/2 раз медленнее, чем у точно такого же, абсолютно покоящегося в пространстве, наблюдателя.

Таким образом при нашем подходе к данной проблеме приходим к выводу, что эффект Доплера для световых волн вполне объясняется без использования положений СТО. При этом полученные результаты полностью соответствуют результатам экспериментов. И, что самое главное при этом, несут в себе вполне понятный физический смысл и полностью соответствуют нормальной логике.

Исходя из нашей позиции по данному вопросу, нетрудно понять, что поперечный эффект Доплера должен существовать и его посредством аналогичных рассуждений нетрудно рассчитать. Результат полностью соответствует эксперименту, поставленного Айвсом на катодных лучах.

Соответствующим образом можно рассчитать и другие явления, эксперименты, которые на современном этапе объясняются посредством положений теории относительности.

Возвращаясь к эффекту Доплеру, проанализируем результаты, полученные А. Эйнштейном в §7 своей статьи «К электродинамике движущихся тел» при изложении теории эффекта Доплера для электромагнитных волн. Решая поставленную задачу, он [3, c.35] «…применив найденные в §6 формулы преобразования напряжённостей электрического и магнитного полей, а также полученные в §3 формулы преобразования координат и времени…», получает значения величин, характеризующих [3, с.35] «…свойства … волн, когда они исследуются наблюдателем, находящимся в покое относительно движущейся системы…». В предыдущей нашей статье [1, c.125 − 139], нами было высказано утверждение, что даже беглого взгляда достаточно для того, чтобы понять ошибочность подобных преобразований. В этой связи вспомним, что электрические и магнитные составляющие силовых характеристик электромагнитного поля находятся в соотношении: E ~ vB.

Из сказанного следует, что полученные на основе этого результаты не могут быть правильными. В данном случае проанализируем полученную А. Эйнштейном формулу, описывающую эффект Доплера. Цитируем [3, с.35]:

«Возьмём наблюдателя, движущего со скоростью v относительно бесконечно удалённого источника света, частота которого равна ν. Из уравнения для ω^׳ вытекает, что если угол между линией, соединяющей источник света с наблюдателем, и скоростью наблюдателя, отнесённой к координатной системе (покоящейся относительно источника света), равен φ, то воспринимаемая наблюдателем частота ν ^׳ света даётся следующей формулой:

ν ^׳ = ν [1 – (v/V) cosφ] / .

Это и есть принцип Доплера для любых скоростей. При φ = 0 формула принимает более простой вид:

ν ^׳ = ν .

Мы видим, что, в противоположность обычному представлению, при v = − ∞ частота ν = ∞».

Можно было бы, конечно, не придавать большого значения положению, высказанному А. Эйнштейном в приведённой выдержке, относительно условия равенства бесконечности скорости движения наблюдателя со знаком минус. Однако здесь, с нашей точки зрения, имеются несколько важных, в русле анализа теории относительности, моментов. Первое это то, что это условие (v = − ∞) приводит основоположник теории относительности, в основе которой, как один из принципов, лежит положение о предельной скорости передачи любого взаимодействия (принцип близкодействия), равной скорости распространения света. Несомненно, с научной точки зрения это не допустимо. Во-вторых, если пропустить только что озвученное замечание, из последней формулы приведённой выдержки следует, что при стремлении скорости движения наблюдателя достигнуть и превзойти скорость света (условие 0 ≤ v ≤ − ∞) с физической и реальной точки зрения получаем абсурдные результаты.

Следующее, и здесь, наверное, самое главное. Предположим, что за бесконечность А.Эйнштейн принимает скорость света. (И это действительно так, что следует из его замечания [3, с.27] «…скорость света в нашей теории физически играет роль бесконечно большой скорости…»). Тогда предыдущие наши замечания пока оставим в стороне.

Общеизвестно, что скорость тела есть величина векторная. Модуль скорости (т.е. её численное выражение) может принимать только положительные значения. Вектор же скорости, т.е. её направление, может иметь как положительное, так и отрицательное значение относительно некоторого другого, наперёд выбранного направления. Например, к наружной нормали направления распространения фронта световой волны от источника к наблюдателю. В контексте приведённой выдержки, угол φ есть угол между прямой, соединяющей источник света и наблюдателя, и вектором скорости движения наблюдателя. Безотносительно к направлению распространения фронта световой волны, т.е. при сближении или отдалении источника и наблюдателя. При равенстве нулю значения угла φ вектор скорости движения наблюдателя будет лежать на прямой, соединяющей источник света и наблюдателя. Тогда знак минус в выражении для скорости (при v = − ∞, т.е. при v = − c) означает, что направление вектора скорости движения наблюдателя противоположно … направлению вектору скорости движения наблюдателя! Такова логика А. Эйнштейна при описании рассматриваемого эффекта.

Совпадение результатов описания эффекта Доплера посредством положений теории относительности и нами предложенным решением указанного явления объясняется, как не трудно понять, применением множителя β = (1 – v²/c²)^1/2. Это с математической точки зрения. С физической же точки зрения в этих двух подходах имеются огромнейшие, фундаментального уровня, различия, о которых мы говорили ранее.

Рассматривая эффект Доплера, как одно из явлений природы, описываемых СТО, мы преследовали здесь двоякую цель. Первое это показать, что эти явления, эффекты можно объяснить и описать методами, отличными от упомянутой теории. Второе, и это здесь самое главное, проанализировать образ научного мышления А. Эйнштейна, ибо в этом, по нашему мнению, заложена основа того, что привело к неверному восприятию им окружающей физической реальности. И в конечном итоге к созданию неверных теоретических построений.

Продолжая, в этой связи обратимся к вопросу о системах отсчёта. В данном случае это имеет наиважнейшее значение. Как известно, в общем случае, системой отсчёта называется система тел или частей одного и того же тела с совмещёнными с ними координатными осями. Применение понятия систем отсчёта играет большую роль для описания состояния движения или покоя того или иного физического объекта, изменения этих состояний под действием каких-либо силовых факторов. Упомянутые тела, составляющие основу системы отсчёта, а также сами исследуемые объекты, могут носить как абстрактный, так и реальный физический характер. В первом случае при рассмотрении и описании того или иного явления тела рассматриваются отвлечённо от физической реальности, как некие фигуры, по существу как математические объекты. В противовес этому, во втором случае все тела, находясь в реальном физическом пространстве, наделены реальными физическими свойствами и объективно взаимодействуют друг с другом. По нашему глубокому убеждению, основанному на анализе многих ныне существующих научных разработок, подобные подходы к решению научных физических задач с использованием понятий систем отсчёта действительно существуют. В частности, абстрактный подход в своих научных исследованиях зачастую использовал и А. Эйнштейн, что, естественно, не допустимо. Создание Специальной теории относительности, в ошибочности которой мы нисколько не сомневаемся, является ярким тому примером. Действительно, при справедливости второго постулата теории (в чём нет никаких сомнений) и при утверждении о реальном существовании пространственно-временного континуума, следует, что каждая система отсчёта имеет своё пространство со своим «течением» времени. Несомненно, это является, мягко говоря, абсурдом, ничего не имеющего общего с реальностью. Такое возможно только при абстрактном видении рассматриваемых в теории явлений.

А.Эйнштейн и сам признавался в том, что иногда не мог получить удовлетворительные ответы при стремлении объяснить некоторые явления посредством логических построений физического характера. Применяя же для описания указанных явлений математические методы, получал вполне приемлемые результаты. По нашему мнению всё это связано с неполнотой понимания глубинной сущностью исследуемых процессов и явлений. А отсюда невозможностью объяснить их посредством реального, а не абстрактного мышления.

Другим примером, и это самый главный побудительный мотив написания предлагаемой статьи, в этом отношении является Общая теория относительности.

Здесь мы не будем детально анализировать указанную теорию, рассмотрим только её основу. Этого будет достаточно для подтверждения нашей позиции. А заодно для показа ошибочности и этой, общей части, так называемой, теории относительности.

С этой целью обратимся к статье А. Эйнштейна «О влиянии силы тяжести на распространение света» и проанализируем её. В §1 «Гипотеза о физической природе гравитационного поля» этой статьи он пишет [3, с.46]:

«Пусть в однородном поле тяжести (ускорение силы тяжести γ) находится покоящаяся координатная система K, которая ориентирована так, что силовые линии поля идут в отрицательном направлении оси z. Пусть в пространстве, свободном от гравитационных полей, находится вторая координатная система K´, которая равномерно ускоренно (с ускорением γ) движется в положительном направлении своей оси z.»… «Материальные точки, которые не подвергаются влиянию со стороны других материальных точек, движутся относительно K, как и относительно K´, в соответствии с уравнениями

d²x_y / dt² = 0, d²y_y / dt² = 0, d²z_y / dt² = - γ. »

Обратим внимание здесь на координатную систему «…K´, которая равномерно ускоренно … движется в положительном направлении своей оси z.» При этом «…материальные точки … движутся … относительно K´…» в соответствии с вышеприведёнными в тексте уравнениями. Отметим, что процесс этот рассматривается происходящим в пространстве. Отсюда следует, (в соответствии со смыслом всей выдержки из текста статьи), что если координатная система K´ движется в пространстве с указанным ускорением, то материальные точки при этом покоятся. Если же в пространстве движутся материальные точки с этим ускорением γ, то покоится система координат K´. Таково налицо первое противоречие.

Исходя из самого смысла статьи, рассматриваются материальные точки в одном случае находящиеся в системе отсчёта, связанного с телом, обладающим гравитационным полем, а во втором случае связанными с системой отсчёта, движущейся равноускоренно. Отсюда следует однозначно, что сами материальные точки во втором случае покоятся относительно тел, составляющих основу системы отсчёта, то есть не испытывают никакого ускорения. А, следовательно, не подчиняются приведённым выше уравнениям.

Вообще нужно отметить, если рассматривать движение материальных точек, что изменение состояния движения или покоя любого тела возможно по существу только двумя способами: или посредством того или иного преобразования внутренней энергии, или же посредством того или иного внешнего воздействия. В данном случае рассматривается поведение системы материальных точек в гравитационном поле и эта же система материальных точек при равноускоренном движении. Отсюда ясно, что равноускоренное движение при этом может рассматриваться только в результате внешнего воздействия. Все материальные точки, как физические тела, обладают массой и, следовательно, в любом случае, подвержены гравитационному воздействию со стороны других тел. Точно так же как и наоборот: источником гравитационного поля могут быть только материальные тела и их системы. У А. Эйнштейна же, судя по вышеприведённой выдержке из статьи, «… материальные точки … не подвергаются влиянию со стороны других материальных точек …». И это второе противоречие.

Возможно, понимая всё это, А. Эйнштейн привязывает движущиеся материальные точки к системе отсчёта K´, в которой они покоятся, и рассматривает равноускоренное движение этой системы отсчёта с указанными материальными точками.

Естественно при этом возникает вопрос об относительности движения этой системы. С этой целью вводится система отсчета K₀ и относительно этой системы и рассматривается движение системы K´. В этой связи, обосновывая допущение о равноценности систем K и K´, автор теории относительности обсуждает [3, с.49] «… процесс переноса энергии излучением …, находясь в некоторой системе K₀, которая не обладает ускорением». С этой целью берутся две физические системы тел S₁ и S₂, снабжённые измерительными приборами, расположенными на оси Z, как системы K, так и системы K´. Далее полагая [3, с.49], «… что в тот момент, когда энергия излучения E₂ переносится из S₂ в S₁, система K´ обладает относительно системы K₀ скоростью, равной нулю. Лучи достигнут системы S₁ спустя время h/c (в первом приближении). В этот момент система S₁ обладает относительно K₀ скоростью γh/c = υ. Поэтому, согласно обычной теории относительности, достигающее S₁ излучение имеет не энергию E₂, а большую энергию E₁ …».

Проанализируем описанную ситуацию. Здесь, по нашему мнению, крайне необходимо, как и в предыдущей своей статье [1, с.125−139], для аргументации рассуждений, привести ещё раз выдержку о движении лифта из работы А. Эйнштейна и Леопольда Инфельда «Эволюция физики. Развитие идей от первоначальных понятий до теории относительности и квантов» следующего содержания [3, с.278]: «… Представим себе, что световой луч входит в лифт горизонтально через боковое окно и спустя очень короткое время достигает противоположной стены. Посмотрим, каковы будут предсказания обоих наблюдателей относительно пути луча.

Внешний наблюдатель, который считает, что лифт находится в ускоренном движении, утверждал бы: световой луч входит в окно и движется горизонтально вдоль прямой с постоянной скоростью по направлению к противоположной стене. Но лифт движется вверх, и за время, в течение которого свет доходит к стене, лифт изменит своё положение. Поэтому свет упадёт в точку, расположенную не точно напротив точки его входа, а немного ниже… Смещение будет очень небольшим, но тем не менее оно существует, и световой луч проходит относительно лифта не вдоль прямой, а слабо искривлённой линии. Это вызвано тем, что за то время, пока луч проходит внутри лифта, сам лифт смещается на некоторое расстояние.

Внутренний наблюдатель, который считает, что на все объекты в лифте действует поле тяготения, сказал бы: ускоренного движения лифта нет, а есть лишь действие поля тяготения…». «… Луч света будет искривляться в поле тяготения точно так же, как искривляется траектория тела, брошенного горизонтально со скоростью, равной скорости света…». Тем самым выводы внутреннего наблюдателя [3, с.279] «…были бы точно такими же, как и выводы внешнего наблюдателя…».

Исходя из позиции А. Эйнштейна, выраженной в приведённых выше выдержках, и которая проанализирована нами в нашей первой статье, следует, что луч света в движущейся равноускоренно системе отсчёта K´ проделает от системы S₂ к системе S₁ путь меньший, чем h, и, следовательно, затратит промежуток времени меньший, чем h/c. При этом первое приближение, как выражается А. Эйнштейн, то есть сокращение расстояний в направлении движения системы K´, здесь ни при чём. Уменьшение же пройденного лучом света расстояния находится в зависимости равноускоренного движения системы отсчёта K´. Это первое.

Второе. Свяжем с системами отсчёта K и K´, как и у А. Эйнштейна лифты. В системе K первый покоится в гравитационном поле, а второй покоится в движущейся системе K´. Рассмотрим движение луча света, который входит в лифты горизонтально через боковое окно. Пусть в независимые произвольные моменты времени, которые примем за начало отсчёта времени, то есть в t = 0 и t´ = 0 в той и в другой системе отсчёта лучи света входят горизонтально в указанные лифты. В этом случае мы полностью солидарны с автором теории относительности: лучи света достигнут противоположных стенок лифтов не точно напротив их входа, а несколько ниже на величину Δz и Δz´, и их траектории будут представлять из себя слегка искривлённые линии. Дополним эти рассуждения. Пусть мы будем посылать такие же лучи света через определённые, наперёд заданные, произвольные промежутки времени Δt и Δt´. В системе отсчёта K, связанной с гравитационным полем, луч света будет вести себя во все последующие промежутки времени одинаково, то есть отклоняться от горизонтали на одну и ту же величину Δz. При этом для угла [3, с.55] «…отклонения α, которое луч света испытывает …, получаем выражение

α = 1/c²∫(∂Ф/∂n´)ds…»,

что соответствует нашему заключению о независимости углов отклонения от времени.

В движущейся с постоянным ускорением γ системе отсчёта K´ всё обстоит иначе. В этом случае отклонение луча от горизонтали увеличивается пропорционально квадрату величины промежутков времени, прошедших с моментов измерения этих отклонений Δz´. Однако по этому поводу Эйнштейн делает ошибочный вывод: [3, с.55] «…Этот же результат мы могли бы получить и путём непосредственного рассмотрения распространения луча света в равномерно ускоренной системе отсчёта K´, преобразования результата к системе K и затем обобщения на случай гравитационного поля произвольного вида».

Кроме того, процесс движения системы отсчёта K´ рассматривается относительно системы отсчёта K₀, о состоянии движения которой в пространстве ничего не известно. Следовательно, даже на момент t₀ = 0, принятого за начало измерений, возможно отклонение луча от горизонтали на некоторую величину Δz₀´, пропорциональную величине скорости движения в пространстве системы отсчёта K₀.

Таким образом, из рассмотрения процесса переноса энергии из системы S₂ в систему S₁ систем отсчёта K и K´, а также сравнения отклонения от горизонтали луча, идущего перпендикулярно движению, перемещающейся равномерно ускоренно системы отсчёта K´ и системы отсчёта K, связанного с источником гравитации, следует, что эти две системы отсчёта, для электромагнитных процессов по крайней мере, физически не равноценны.

Совместим теперь с системами отсчёта K и K´ лифты (добавим, одинаковые) и поместим в каждый из них наблюдателей. Эти наблюдатели с одной стороны будут субъективно оценивать процессы, происходящие в лифтах, а с другой стороны будут выполнять роль материальных тел, находящихся в этих лифтах. Пусть материальные тела, помещенные в лифт, связанный с системой отсчёта K´, не испытывают воздействия со стороны других тел и полей. В том числе и гравитационного и любого другого поля центральных сил. А, следовательно, лифт движется равноускоренно посредством воздействия со стороны других тел, использующих для этого свою внутреннюю энергию. Тогда все материальные тела, помещенные в лифт, в том числе и наблюдатели, будут всё время « притягиваться» к «полу» лифта. Сами наблюдатели при этом могут предполагать, что они вместе с лифтом находятся в пространстве действия гравитационного поля. Пусть, далее, лифт, связанный с системой отсчёта K, находится в состоянии свободного падения в пространстве действия гравитационного поля, а, следовательно, движется равноускоренно. Тогда все материальные тела, помещённые в лифт, в том числе и наблюдатели, будут находится в состоянии свободного «парения». Сами наблюдатели при этом могут предполагать, что они вместе с лифтом находятся в пространстве в состоянии покоя или равномерного и прямолинейного движения и, тем самым, их система отсчёта инерциальная.

Таким образом, при нахождении систем отсчёта K и K´ физически в одном и том же состоянии движения процессы, происходящие в них, физически являются прямо противоположными. Точно такой же вывод будет и при нахождении обеих этих систем физически в состоянии покоя, соответственно. Отсюда следует, что эти две системы отсчёта, по существу, являются антиподами и, следовательно, в общем случае, не эквивалентны друг другу. Этот же результат следует и из предыдущих наших выводов.

Здесь, однако, надо отметить, что для механических процессов (но не электромагнитных), происходящих в системе отсчёта K, покоящейся в гравитационном поле с ускорением свободного падения γ, и в системе отсчёта K´, движущейся в пространстве равномерно ускоренно с ускорением γ следует эквивалентность указанных систем отсчёта. Это связано с тем, в соответствии с нашими убеждениями, природа гравитации и инерции является единой сущностью фундаментального характера. При этом не существует массы тела тяготеющей и массы тела инертной, а есть только масса тела в этих своих проявлениях. В связи с этим необходимо сказать, что в отличие от мнения Эйнштейна и современных взглядов силы инерции являются реальными, а не фиктивными силами, не фиктивной причиной поведения тел, в том числе движения по инерции. Отсюда следует, что нами полностью отвергается так называемый «принцип Маха».

Электромагнитные явления не вписываются в эквивалентность рассматриваемых здесь систем отсчёта – одну, связанную с гравитационным полем, а другую, равномерно ускоренно движущуюся в пространстве, – по причине отличия этих явлений от механических принципиального, фундаментального характера. Нами предполагается показать всё это в дальнейшем.

Таким образом, подытоживая, можно сделать только один однозначный вывод: использовать законы равноускоренного движения для описания законов гравитации и, соответственно, на этой основе для построения картины Мира, представляется весьма и весьма сомнительным. А для нас, в соответствии с нашими взглядами, вообще не приемлемыми.

Показав здесь несостоятельность теории относительности на фундаментальном уровне, можно перейти к рассмотрению устройства окружающей физической реальности на новой основе.

 

Литература

 

1.                  Мигунов-Миллер С.Н. «К электродинамике движущихся тел»: реальность или фальсификация? / Журнал научных публикаций аспирантов и докторантов, №3(105), 2015, 125−139 с.

2.                  Паули В. Теория относительности: пер. с нем., М., Наука., 1991, 328 с.

3.                  Эйнштейн А. Работы по теории относительности / Альберт Эйнштейн: пер. с нем. и англ., СПб., Амфора, 2008, 330 с.

 

Поступила в редакцию 11.08.2015 г.