Потенциалы движущихся зарядов
Мигунов-Миллер Сергей Николаевич.
В статье проанализирован вывод формулы Лиенара и Вихерта по определению скалярного потенциала, создаваемого движущимся произвольным образом заряда. Показаны ошибки логического порядка, допущенные при этом, что, в конечном счёте, привело к неверному результату. В связи с этим показан правильный вывод формулы по определению потенциала, создаваемого движущимся заряженным телом.
Ключевые слова: скалярный потенциал, движущийся точечный заряд, кванты взаимодействия, запаздывающие потенциалы.
Как известно, формулы преобразования Лоренца берут своё начало с изучения движения электрического заряда, то есть с электродинамики. В свою очередь формула определения потенциала от движущегося с произвольной скоростью заряда была выведена Лиенаром и Вихертом и носит их имя. Следовательно, правильность или неправильность вывода этих формул, а также правильность или неправильность сделанных выводов при изучении этих формул подтверждают или же ставят под сомнение, по крайней мере, математическую основу Специальной теории относительности.
В этой связи проведём анализ формулы Лиенара и Вихерта, определяющей скалярный потенциал движущегося заряда. Именно на неё опирался Лоренц при выводе формулы определения скалярного потенциала, создаваемого зарядом, движущегося с постоянной скоростью.
В литературе очень часто при выводе формулы Лиенара и Вихерта используется понятие интервала и, соответственно этому, понятие 4-х векторов. (К примеру [1.210 – 213]). Как было показано нами ранее, применение этих понятий для доказательства тех или иных положений является неоднозначным, то есть некорректным и поэтому при анализе формулы Лиенара и Вихерта будем пользоваться источниками, которые не используют эти понятия.
В соответствии с только что сказанным, для решения поставленной задачи, рассмотрим [2.158-162]. Не будем полностью цитировать данный материал, а приведём лишь посылочные положения, чертёж, поясняющий рассуждения автора, и конечный результат, полученный при этом.
Согласно начальным положениям, имеем [2.158]:
«Попробуем подсчитать в точке (x1, y1, z1) скалярный потенциал φ(1), создаваемый точечным зарядом (вроде электрона), движущегося любым, каким угодно образом. Под «точечным» зарядом подразумевается очень маленький заряженный шарик, такой маленький, как только можно себе представить, с плотностью заряда ρ(x,y,z). Потенциал φ можно найти из…» формулы:
ρ(2,t – r12/c)
«… φ(1,t) = (1/4πε0) ∫ ____________ dV2 … ». (1).
r12
Далее: [2.159]
«…я сперва приведу расчёт для «точечного» заряда в форме небольшого заряженного кубика, который движется к точке (1) со скоростью v…».
Здесь отобразим рис. 1, который соответствует полностью тому, что приведён в рассматриваемом параграфе (фиг.21.5).
«Сторона куба будет а, это число пусть будет много меньше r12 [расстояние от центра заряда до точки (1)].
Чтобы оценить величину интеграла (1), мы вернёмся к основному определению, запишем его в виде суммы:
ρi ΔVi
Σ ________, (2)
i ri
где ri – расстояние от точки (1) до i-го элемента объёма ΔVi, а ρi - плотность заряда в ΔVi в момент ti = (t – ri/c). Поскольку все ri >> a, удобно будет выбрать все ΔVi в виде тонких прямоугольных ломтиков, перпендикулярных к r12» (рис. 1).
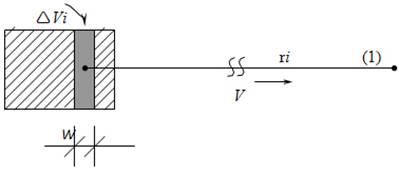
Рис. 1.
Продолжая [2.159]:
«Предположим, что мы начали с того, что взяли элементы объёма ΔVi, некоторой толщины w, много меньшей а.
Отдельные элементы объёма будут выглядеть так, как показано на…» рис. 2. «…Их нарисовано гораздо больше, чем нужно, чтобы закрыть весь заряд. А сам заряд не показан, и по весьма существенной причине. Где его нужно нарисовать? Ведь для каждого элемента объёма ΔVi нужно брать ρ в свой момент ti = (t – ri/c). Но раз заряд движется, то для каждого элемента объёма ΔVi он окажется в другом месте!
Начнём, скажем, с элемента объёма 1на…» рис. 2а, …»выбранного так, чтобы в момент t1 = (t – r1/c) «задняя» грань заряда пришлась на ΔVi…» (рис. 2.б). «…Тогда, вычисляя ρ2ΔV2, нужно взять положение заряда в несколько более позднее время t2 = (t – r2/c) и заряд к этому времени сместится в положение, показанное на…» рис. 2.в. «…Так же будет с ΔV3, ΔV4 и т.д. Вот теперь можно подсчитать сумму».
Далее идут логические и математические построения, которые в конечном итоге приводят к формуле определения потенциала от заряда, движущегося произвольным образом:
q
φ(t) = ____________________________ (3)
4πε0r´[1 – (V r / c)]зап
Или в общем виде
q
φ(t) = ____________________________ (4).
4πε0[r – (V·r / c)]зап
Глядя на формулы (3) и (4) сразу же бросается в глаза отсутствие зависимости величины скалярного потенциала в точке (1) от размера самого заряда (это признаётся и сторонниками правильности формулы Лиенара и Вихерта). Несомненно, это противоречит нормальной логике. Это первое. Второе заключается в том, что, как можно заметить, сначала сам заряд делится на некоторое количество элементов толщиной W (допустим, это количество равно n), а затем на траекторию движения заряда накладывается матрица, каждый элемент которой имеет толщину W. Эта матрица имеет N произвольных элементов. И именно относительно этой абстрактной матрицы ведутся дальнейшие логические и математические суждения и построения. Заряд же здесь выполняет не главную, а второстепенную роль, так как, согласно приведённому тексту (и рис.2), каждый элемент объёма (заряда) накладывается на распределение заряда (на матрицу). Это является принципиально неверной посылкой.
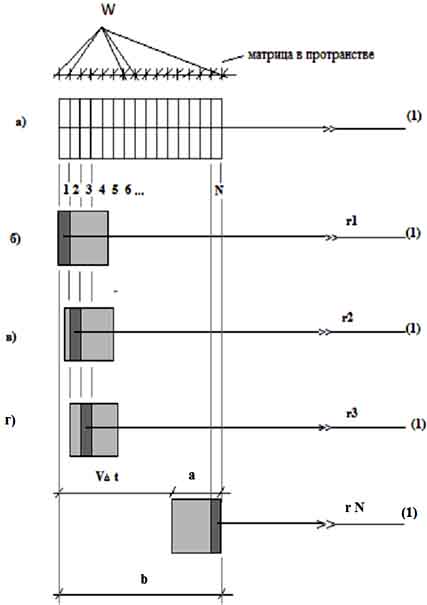
Рис. 2.
Действительно, как следует из логики авторов (и это отображено на рис.2, соответствующему фиг. 21.7 [2.160]), необходимо брать тот ломтик невещественной, абстрактной матрицы, который соответствует моменту времени ti = (t – ri/c), следующий за предыдущим. Здесь, кроме того, нужно помнить, что в любом случае c >>v. А отсюда, к примеру (и это тоже видно из этого рисунка или же соответствующей фигуры, а также и из нормальной логики), при вычислении ρ2ΔV2 по любому берётся часть заряда, который уже брался при вычислении ρ1ΔV1. То есть здесь происходит наложение реального заряда одного ломтика на другой. Другими словами, часть реального заряда ломтика 1 дважды присутствует при вычислениях. И так далее. Но это совершенно не допустимо.
Как же должны вестись рассуждения, применительно к данному случаю. Прежде всего, отметим следующее. Несмотря на небольшие размеры заряженного тела, относительно расстояния от этого заряда до точки (1), в которой необходимо определить скалярный потенциал в некоторый момент времени, различные части этого заряда в один и тот же объективный момент времени всегда находятся в различных частях пространства. Покоится ли данное заряженное тело или же движется. Далее отметим, что заряды в этом заряженном теле распределены равномерно по всему объёму. И, в принципе, разделить такое тело можно (условно, для решения поставленной задачи) только на количество частей, не превышающего величины общего заряда данного тела, кратного общепринятой (и реально существующей) единицы заряда.
Пусть заряд движется к точке (1) так же, как и в приведённом примере и изображённом на рис.1, со скоростью V. Так же, как и в приведённом примере пусть это будет кубик со сторонами равными а, а передняя и, соответственно, задняя грани кубика перпендикулярны вектору скорости. Разделим этот кубик условно на ломтики, толщиной W с величиной заряда в каждом кратного единице заряда, т.е. величина заряда каждого ломтика будет ne = q, а заряд всего кубика будет Q = Nq = Nne, где N – количество ломтиков, на которые разделён кубик. Пусть также r(1)N >> а, где r(1)N – расстояние от точки (1), где определяется потенциал, создаваемый движущимся зарядом до N – ого ломтика. Будем считать, что заряды в ломтиках сосредоточены в их геометрических центрах, т.е. лежат на одной прямой, соединяющей точку (1) с центрами ломтиков.
Так как заряженный кубик движется к точке (1) и необходимо определить скалярный потенциал, создаваемый этим зарядом в строго определённый момент времени, то становиться очевидным следующее. Вследствие конечности скорости передачи взаимодействия, для каждого ломтика нужно брать свой момент времени испускания кванта взаимодействия. Только в этом случае испущенные ломтиками кванты достигнут точки (1) в один и тот же момент времени, т.е.
ti исп = ri / c, (5)
где ti исп – время испускания кванта взаимодействия от i-ого ломтика; ri – расстояние от точки (1) до i-того ломтика в момент испускания кванта взаимодействия этим i-тым ломтиком.
Очевидно, вследствие движения кубика к точке (1), наименьшее из расстояний от точки (1) будет соответствовать расстоянию от искомой точки до ближайшего по движению ломтика, который на рис. 3.а обозначен цифрой 1. К моменту испускания кванта взаимодействия этим последним (относительно времени испускания) ломтиком, кванты взаимодействия от предшествующих ломтиков должны достигнуть центра этого ломтика. Как отмечалось выше, только в этом случае получим величину скалярного потенциала от всего заряженного кубика в строго определённое время – время, когда производятся измерения.
То же самое рассуждение справедливо и для второго, т.е. следующего за первым по нашей классификации ломтиком. На момент испускания кванта взаимодействия этим ломтиком, все кванты взаимодействия от предшествующих ломтиков должны достигнуть центра этого второго ломтика (рис. 3.б). И так далее до последнего ломтика.
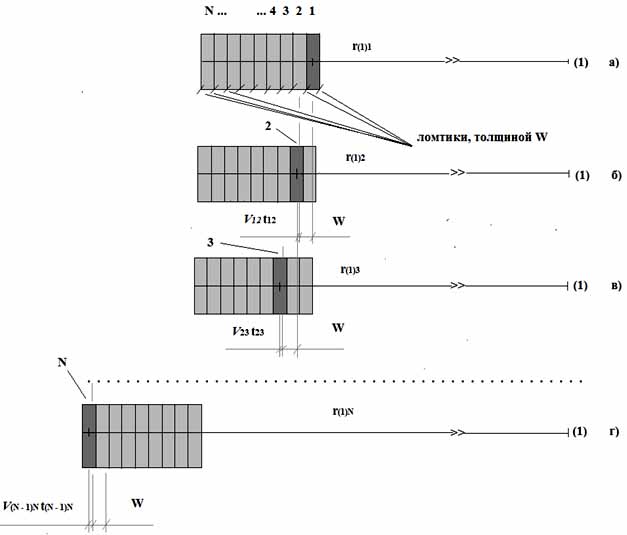
Рис. 3.
Согласно нашим рассуждениям, запишем
r(1)2 = r(1)2 + (W + V12 t12), (6)
где V12 – скорость кубика на момент испускания кванта взаимодействия от второго ломтика и до момента достижения этим квантом центра первого ломтика; t12 – время движения кубика из положения, когда был испущен квант взаимодействия от второго ломтика до момента достижения этим квантом взаимодействия центра первого ломтика и, соответственно, момента испускания кванта взаимодействия от первого ломтика.
Естественно при этом должно выполняться условие:
W + V12 t12 = ct12 (7)
Откуда, решая относительно t12 , получим
t12 = W/(c – V12) (8)
Тогда
r(1)2 = r(1)1 + [W/(1 – V12/c)] (9)
Соответственно для r(1)3 имеем
r(1)3 = r(1)2 + (W + V23 t23); W + V23 t23 = ct23;
t23 = W/(c – V23); r(1)3 = r(1)2 + W/(1 – V23/c);
r(1)3 = r(1)1 + [W/(1 – V12/c)] + [W/(1 – V23/c)] (10)
Для r(1)N имеем:
r(1)N = r(1)1 + [W/(1 – V12/c)] + [W/(1 – V23/c)] +…+ [W/(1 – V(N -1),N/c)] (11)
Тогда, переходя к основному определению интеграла (1), т.е. используя (2), получим:
ρiΔVi ρ1ΔV1 ρ2ΔV2
φ(1,t) = [1/4πε0]Σ __________ = [1/4πε0][ ___________+ ______________________________ +
ri r(1)1 r(1)1 + [W/(1 – V12/c)]
ρ3ΔV3
+ __________________________________________+
r(1)1 + [W/(1 –V12/c)] + [W/(1 – V23/c)]
ρNΔVN
+ … + _______________________________________________________________________ ] (11)
r(1)1 + [W/(1 – V12/c)] + [W/(1 – V23/c)] + … + [W/(1 – VN – 1, N/c)]
Вследствие равномерности распределения общего заряда в кубике и одинаковости элементарных объёмов ломтиков (по принятому условию), имеем:
ρ1ΔV1 = ρ2ΔV2 = ρ3ΔV3 = … = ρNΔVN = q (12).
И тогда (11) принимает вид:
qi q q
φ(1,t) = [1/4πε0]Σ _________ = [1/4πε0][ _______ + ________________________ +
ri r(1)1 r(1)1 + [W/(1 – V12/c)]
q
+ __________________________________________+
r(1)1 + [W/(1 –V12/c)] + [W/(1 – V23/c)]
q
+ … + _______________________________________________________________________] (13)
r(1)1 + [W/(1 – V12/c)] + [W/(1 – V23/c)] + … + [W/(1 – VN – 1, N/c)]
Отметим, что в общем виде все кванты взаимодействия от ломтиков (частей) заряженного кубика (тела) на момент испускания последнего кванта наиболее ближним по движению к точке, в которой определяется скалярный потенциал, должны лежать на поверхности сферы. Центром этой сферы является искомая точка, а радиус сферы есть расстояние от этой точки до центра последнего (в смысле времени испускания кванта взаимодействия) ломтика (части) заряженного кубика (тела) (рис. 4).
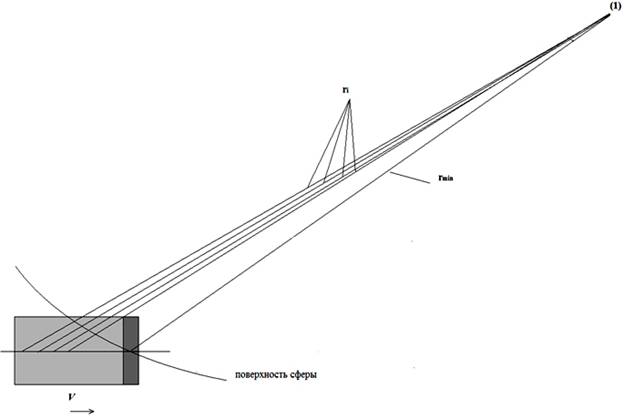
Рис. 4.
Соответственно этому, в формуле (13) скорости в каждый отдельный промежуток времени есть проекции этих скоростей на радиусы - векторы, соединяющие точку, где определяется потенциал, с центрами частей заряженного тела в соответствующие моменты времени испускания кванта взаимодействия той или иной частью тела.
Рассмотрим здесь случай прямолинейного и равномерного движения данного заряженного тела. Из этого следует, что V12 = V23 = … = VN – 1, N =V. Тогда запишем:
qi q q
φ(1,t) = [1/4πε0]Σ _____ = [1/4πε0][ _______ + _____________________ +
ri r(1)1 r(1)1 + W/(1 – V/c)
q q
+ _______________________ + … + ____________________________] (14)
r(1)1 + 2W/(1 – V/c) r(1)1 + (N – 1)W/(1 – V/c)
Как нетрудно понять, слагаемые в знаменателях дробей в (14), являющихся расстояниями от искомой точки (1) до ломтиков в соответствующие моменты времени, представляют собой прогрессию. Отсюда мы можем положить, что при равномерном распределении заряда в заряженном теле,
Q
φ(1,t) = [1/4πε0] _____________________ (15)
r(1)1 + a/2(1 – V/c)
Здесь мы исходим из того, что размеры всего тела намного больше, чем размеры частей, на которые разбивается тело, т.е. что a >> W; размеры частей настолько малы, что r(1)1 по существу есть расстояние от точки (1) до ближайшей к этой точке грани заряженного тела. Сам заряд Q, исходя из смысла вышесказанного, при этом сосредоточен в геометрическом центре заряженного тела и представляет собой сумму всех элементарных зарядов q, на которые это тело разбивается.
Сравнивая (4) и (15) приходим к заключению, что, несмотря на некоторую схожесть, эти формулы явно отличаются друг от друга, причём принципиально.
В формуле (15) отражается тот факт, что потенциал от движущегося заряженного тела зависит от его пространственных размеров, что, конечно же, соответствует элементарной логике, в отличие от формулы (4). Сам вывод формулы (15), несомненно, является логически обоснованным и физически понятным, что не скажешь о формуле (4).
Формулу (15) по определению потенциала от движущегося заряда можно получить при непосредственном интегрировании (1). Для равномерного и прямолинейного движения заряда это более чем очевидно. При этом только нужно помнить, что заряд в общем случае имеет пространственные размеры и, полагая нахождение всего заряда в геометрическом центре тела, учитывать промежуток времени, необходимый для достижения квантами взаимодействия точки, откуда ведётся отсчёт расстояния от тела до точки, в которой определяется потенциал.
Однако мы преследовали здесь цель показать, кроме всего прочего, наглядно и понятно с физической точки зрения, вывод формулы по определению потенциала, создаваемого движущимся зарядом.
Отметим следующее. Если принять, что полученная здесь нами формула по определению потенциала от равномерно движущегося заряда верна, в чём мы абсолютно ни сколько не сомневаемся, то становится ещё более очевидным ошибочность положений Специальной теории относительности. Действительно, сторонники указанной теории для вывода рассматриваемой формулы используют понятие интервала и 4-х векторов в трактовке теории, получая при этом, с нашей точки зрения, неверный результат. А именно формулу (4).
Вывод формулы для определения потенциала от движущегося заряда в правильном виде необходим и важен не только сам по себе, т.е. соответствующим физическим реалиям в этой части, но в ещё значительно большей степени эта формула важна с фундаментальной точки зрения для понимания некоторых определяющих атрибутов материи. Показать это мы предполагаем впоследствии. Но для этого необходимо определиться с такими наиважнейшими категориями бытия как время и пространство. Современные их толкования ни в какой степени удовлетворять не могут по причине отсутствия чёткости в их определении, размытости этих понятий на физическом фундаментальном уровне.
Литература
1. Л.Д.Ландау, Е.М.Лифшиц. «Теоретическая физика», том 2, «Теория поля», издание шестое, исправленное и дополненное, «Наука», Москва, 1973, стр.504.
2. Р.Фейнман, Р.Лейтон, М.Сэндс «Фейнмановские лекции по физике», том 6, «Электродинамика», перевод с английского, «Мир», Москва,1977г., стр.350.
Поступила в редакцию 16.11.2015 г.