Компенсация движения в цифровых динамических видеоизображениях на основе векторных полей
Калистратов Дмитрий Сергеевич,
кандидат технических наук, ассистент кафедры радиоэлектроники Тульского государственного университета.
На сегодняшний день компенсация движения в динамических изображениях активно используется видеокодеками [2, 3, 4], в том числе, в составе цифровых телевизионных систем. Видеокодеки, в свою очередь, применяются для снижения объёма передаваемой информации с целью уменьшения энергетических затрат на передачу сигнала на расстояние. При этом, в общем случае, чем лучше скомпенсировано движение фрагментов в различных по времени кадрах видеопотока, тем короче код видеоизображения и тем меньше энергии расходуется на его передачу по каналам связи [4].
Компенсация движения в современных видеокодеках ведётся, как правило, на фрагментарном уровне [4]. Каждый кадр при этом разбивается на более мелкие блоки изображения, а в процессе компенсации движения для каждого подвижного блока ищется его наилучшее положение в рамках других кадров видеопотока. При этом, поиск сходных областей изображений ведётся только по перебору вариантов с поступательным движением (сверху вниз и слева направо).
Наиболее уязвимым с точки зрения подобного стандартного поискового алгоритма является вращательная степень свободы пространственного объекта при его движении вокруг оси перпендикулярной плоскости кадрового изображения.
Для того, чтобы учесть указанную вращательную степень свободы, необходимо было бы на программном уровне добавить ещё один вложенный цикл, который дополнительно к поступательным смещениям перебирал бы возможные значения угла поворота для каждого подвижного блока.
Однако, вместе с тем, очевидно, что требовательность такого алгоритма к производительности обслуживающего вычислительного устройства возрастёт ровно во столько раз, сколько возможных значений угла поворота блоков будет проверять алгоритм.
По этой причине с точки зрения работы видеокодека в режиме on-line такой подход недопустим, поскольку приводит к существенному нарушению плавности воспроизведения изображений на стороне декодирования.
Одним из возможных вариантов решения данной проблемы является использование для анализа и прогнозирования движения математического аппарата векторных полей [1]. Так, например, в плоскости кадрового изображения вращательное движение фрагментов может описываться вихревым векторным полем скоростей (рисунок 1).
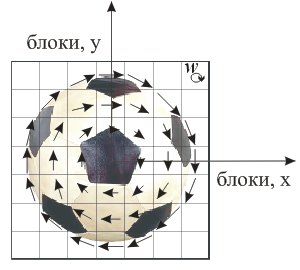
Рис. 1. Вихревое поле скоростей движения фрагментов проекции подвижного объекта.
В зависимости от угловой скорости w, векторы данного поля могут иметь различную длину. Кроме того абсолютные значения скоростей возрастают при переходе от центра к краям проекции.
Если представить скоростные проекции данного векторного поля раздельно, то можно отметить, что линейная скорость движения блоков вдоль оси x возрастает с ростом ординаты блока, а линейная скорость движения по оси y падает с ростом абсциссы блока (рисунок 2).
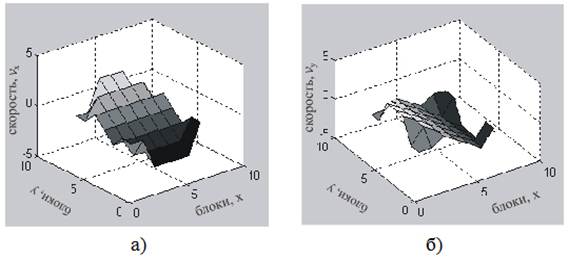
Рис. 2. Графики зависимости проекций линейных скоростей фрагментов проекции: а) для оси x; б) для оси y.
Для того, чтобы определить характер векторного поля (идентифицировать его) можно использовать несколько опорных блоков и проанализировать характер их движения (рисунок 3). Координаты каждого блока, в этом случае, можно представлять координатами одной из его точек.
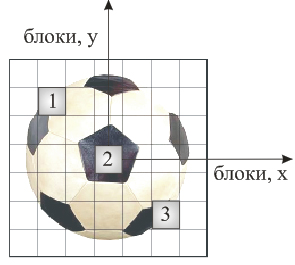
Рис. 3. Выбор опорных блоков для проведения векторного анализа и идентификации типа поля.
К примеру, для идентификации вихревого векторного поля можно использовать пару совместных условий на основе градиентов (векторов частных производных):
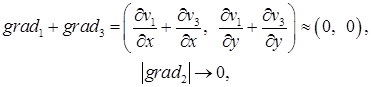
где: v1, v2, v3 – линейные скорости в координатных точках соответствующих опорных блоков. Первое условие состоит в том, что сумма градиентов первого и третьего опорных блоков равняется нуль-вектору (поскольку указанные градиенты противонаправлены и равны по абсолютным значениям). Второе условие отражает неподвижность блока, находящегося в центре вращения.
Для идентификации вихревого векторного поля можно использовать и другую пару совместных условий на основе роторов (векторов завихрения):
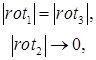
Таким образом, через такие математические объекты, как градиент и ротор, можно устанавливать характер векторного поля скоростей фрагментов больших по площади проекций.
Суть такого подхода состоит в том, что идентификация типа и параметров векторного поля проводятся по малому количеству блоков, а само поле впоследствии охватывает большое количество соседних блоков. Процесс прогнозирования движения при этом значительно ускоряется.
Литература
1. Гаврилов В.Р., Иванова Е.Е., Морозова В.Д. Кратные и криволинейные интегралы. Элементы теории поля. – М.: Изд-во МГТУ им. Баумана,2003. – 496с.
2. Минаков Е.И. Калистратов, Д.С. Режимы формирования кадровых прогнозов в компенсаторах движения видеообъектов / Е.И. Минаков, Д.С. Калистратов // Известия Тул ГУ. Технические науки. Вып.11 Ч.2. Тула: Изд-во ТулГУ, 2012. С.188–193.
3. Патент на изобретение № 2552139. Способ компенсации движения в цифровых динамических видеоизображениях / Минаков Е.И., Калистратов Д.С. Приоритет от 16.12.2013, опубл. 29.04.2015.
4. Ричардсон Я. Видеокодирование. Н.264 и МРЕG-4 – стандарты нового поколения. – М.: Техносфера, 2005. – 368с.
Поступила в редакцию 25.05.2016 г.