Полная формула теоремы Пифагора о прямоугольном треугольнике

Юлдашев С. А.,

старший преподаватель,

Исломов Ё. А.,

старший преподаватель,

Садуллаева М. З.,

преподаватель.

Ташкентский институт проектирования строительства и эксплуатации автомобильных дорог.

Формула теоремы Пифагора (ок. 500 г. до н.э.) известна человечеству очень давно, задолго до самого Пифагора. Её использование находят у египтян ещё около 2300 г. до н. э., а у вавилонян в тексте, который относят к 2000 году до н. э., приводится приближённое вычисление гипотенузы равнобедренного прямоугольного треугольника [1]. Доказательства теоремы Пифагора исчисляются сотнями, что указывает на её фундаментальность. Действительно, в своё время – две с половиной тысячи лет назад – она была вершиной математики. Но время движется вперёд, знания умножаются, задачи встают всё более сложные. И это заставляет посмотреть, насколько отвечает нынешним задачам существующее решение теоремы Пифагора.

Итак, имеем формулу теоремы Пифагора для прямоугольного треугольника на плоскости, которая записывается в виде [1]:

                                                                                                      (1)

где a и b – катеты, а c – гипотенуза прямоугольного треугольника. В алгебраической трактовке a, b и c – это числа. На первый взгляд всё очень просто. А множество решений доказательства этой теоремы – алгебраические, геометрические и даже дифференциальные – говорят о её правильности и неоспоримости. Для наглядности приведём доказательство теоремы (1) через радиус описанной окружности.

Итак, дано: прямоугольный треугольник на плоскости, вписанный в окружность радиуса r (рис.1).

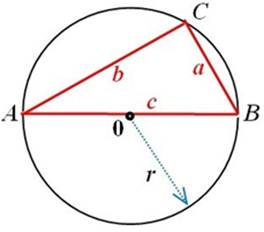
Рис. 1. Прямоугольный треугольник, вписанный в окружность радиуса r.

Требуется: доказать, что сумма квадратов длин катетов равна квадрату длины гипотенузы.

Доказательство. Для начала соединяем центр окружности 0 с вершиной прямого угла C как показано на рис.2. Угол при одной из двух других вершин обозначаем буквой φ.

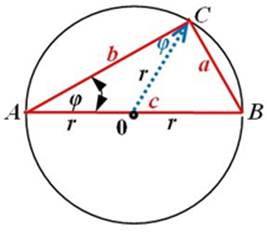
Рис. 2. Прямоугольный треугольник, вписанный в окружность и разделённый на два равнобедренных.

Получаем два равнобедренных треугольника с общей вершиной в точке 0. Из этой точки опускаем на основания равнобедренных треугольников высоты 0m и 0n и получаем 4 равных между собой прямоугольных треугольника (см. рис.3), подобных исходному треугольнику.

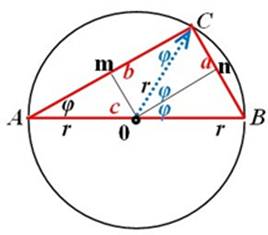
Рис. 3. Прямоугольный треугольник, разбитый на четыре одинаковых прямоугольных треугольника.

Отличительная особенность всех 4-х полученных прямоугольников состоит в том, что у них гипотенузы равны радиусу описанной окружности. Катеты полученных треугольников легко найти через известную гипотенузу (радиус окружности) и угол φ при вершине:

                                                      (2)

Из рис.3 видно, что каждый из катетов исходного треугольника состоит из двух катетов меньших треугольников. Т.е. можно записать, что

 и

                                                                   (3)

Тогда сумма квадратов длин катетов исходного треугольника с учётом того, что , и что , будет равна:

  (4)

Т.е. после упрощений и замен получаем, что для любого прямоугольного треугольника, вне зависимости от величины угла φ при другой вершине:

                                                                                                        (5)

Теорема Пифагора доказана.

Действительно, формула (5) даёт правильный количественный результат. И если бы эта формула не лежала в основе математических действий над векторами, можно было бы такую формулировку считать окончательным результатом теоремы Пифагора. Собственно так и обстоит дело в настоящее время. Однако применять формулу в таком виде для векторных величин совершенно недопустимо – потерялась половина полезной информации.

Чтобы понять, что именно потерялось для векторной алгебры, следует обратить внимание на промежуточный результат формулы (4) – 4r². Ведь это не простое умножение квадрата радиуса на 4. Это сумма квадратыов четырёх разных радиусов, точнее разных радиус-векторов, что хорошо видно на рис. 3, и более наглядно на рис. 4.

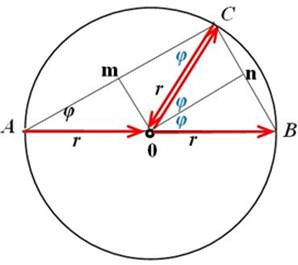
Рис. 4. Прямоугольный треугольник и результирующие радиус-векторы.

Т.е. согласно приведенному выше доказательству, сумма квадратов длин двух катетов прямоугольного треугольника равна сумме квадратов длин четырёх отдельных радиус-векторов описанной вокруг него окружности. Последнее можно записать в виде формулы:

                                             (6)

При этом два радиус-вектора A0 и 0B составляют гипотенузу прямоугольного треугольника, а два дополнительных радиус-вектора C0 и 0C не входят в состав исходного треугольника. Они соединяют центр описанной окружности с вершиной прямого угла. Т.е. результат решения теоремы Пифагора кроме известной из формулы (1) гипотенузы включает в себя два дополнительных радиус-вектора C0 и 0C.

Из диаграмм рис.4 хорошо видно, что дополнительные радиус-векторы направлены в противоположные стороны. Поэтому с формальной точки зрения они не могут влиять на результат, т.к. взаимно компенсируют друг друга:

                                                                                                            (7)

Но если убрать указанные векторы из формулы (6) она преобразуется в следующее выражение:

                                                             (8)

или

                                                                                  (9)

Т.е. если отбросить радиус-векторы 0C и C0, которые не принадлежат сторонам треугольника, то получаем половинчатый результат, который явно не соответствует известной формуле теоремы Пифагора (1). Это значит, что без дополнительных, не принадлежащих сторонам треугольника векторов из формулы (6) теорема Пифагора теряет половину результата. Действительно, дополнительные векторы компенсируют друг друга, но в формулах доказательства теоремы фигурируют не они сами, а квадраты их длин, которые не компенсируются. Поэтому дополнительные векторы являются неявным, но необходимым компонентом формулы теоремы Пифагора. Тогда с учётом выше сказанного и того, что радиус составляет половину от гипотенузы, решение теоремы Пифагора записывается в виде:

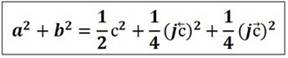                                                         (10)

где первое слагаемое  – это явная или действительная компонента результата, а слагаемые  и  – неявная компонента суммы квадратов длин катетов, буква j – это указание на неявное значение числа или величины. Полученная формула (10) является полной формулой о сторонах прямоугольного треугольника – для алгебраической, геометрической и векторной форм теоремы Пифагора.

Итак, в статье доказано, что существующая формула (1) теоремы Пифагора является упрощённым вариантом её решения, который можно использовать только для количественной оценки результата. Выведена полная формула (10) теоремы Пифагора. Она показывает, что сумма квадратов длин катетов прямоугольного треугольника на плоскости состоит из двух равноправных компонент – действительной или вещественной части и неявной части. Неявная часть может быть выражена в форме мнимых величин [5] или параметров виктори-поля [4]. Это позволяет кроме количественной оценки сделать качественный анализ полученного результата. Поэтому полная формула теоремы Пифагора важна как для математики, особенно раздела векторной алгебры, так и для физики в целом.

Литература

1.                  Ч.Киттель, У.Найт, М.Рудерман, Берклеевский курс физики. т.1, Механика. М., Наука, 1975г.

2.                  Теоретические основы электротехники, Л. А. Бессонов: Высш. шк., 2010г.

3.                  Бабич И.П. "Мощность в электрических цепях переменного синусоидального тока", http://www.sciteclibrary.ru/rus/catalog/pages/12541.html

4.                  Бабич И.П. «Окружность – это комплексная кривая второго порядка», http://sciteclibrary.ru/rus/catalog/pages/13164.html

Поступила в редакцию 28.10.2016 г.