Использование теоретико-игровой модели при формировании соглашений по экологической безопасности

 

Акимова Арина Николаевна,

Мельников Валерий Викторович,

соискатели Санкт-Петербургского государственного университета.

 

1.                  Введение

 

В последние несколько десятков лет многие в мире неоднократно задумывались о проблемах загрязнения окружающей среды и о глобальном влиянии этого загрязнения на климат во многих уголках Земли. Очень часто обсуждения этих проблем приводят к формированию межгосударственных соглашений. Одним из самых известных является «Киотский протокол».

Основной проблемой при обсуждении подобных вопросов является обсуждение снижения вредных выбросов и оценивание потерь при объединении или участии той или иной страны в каком-либо соглашении. Именно это во многом является решающим для многих стран при решении вопроса о вхождении в то или иное соглашение по снижению уровня вредных выбросов.

В данной статье будет представлен один из вариантов математической интерпретации описанной выше проблемы.

 

2.                  Основные обозначения и формирование функции затрат

 

Обозначим через  объем выбросов загрязняющих веществ (в год) с территории i-ой страны, являющейся участником процесса трансграничного взаимодействия. Пусть в этом процессе участвуют n стран, т.е. .

Предположим, что имеется матрица основных направлений трансграничного взаимодействия, в которой каждый элемент  характеризует вклад в загрязнение i-ой страны единичного объема выброса с территории j-ой страны. Тогда уровень загрязнений, попадающих в страну j от трансграничных потоков с территории других стран, можно определить следующим образом [5]: , .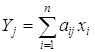

 

Для формирования функции затрат стран, участников трансграничного взаимодействия, введем следующие коэффициенты:

– удельный объем компенсационных величин j-ой стране на единицу объема привнесенного трансграничного загрязнения;

– удельный объем экономического ущерба i-ой стране от единичного объема загрязнения ее территории. (При этом ).

Рассмотрим выпуклую убывающую функцию , описывающую общий объем затрат i-ой страны на поддержание объема выброса вредных веществ, осуществляемого с ее территории, на уровне .

С помощью введенных коэффициентов, функции затрат стран-участников процесса трансграничного взаимодействия (), можно записать в следующем виде:

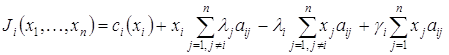.                (1)

 

Такое построение функции затрат учитывает: объем затрат, связанных с регулированием объема выброса (первое слагаемое); общий объем компенсационных выплат, осуществляемых страной другим странам (второе слагаемое); уменьшение затраты данной страны за счет компенсационных платежей, поступающих из других стран (третье слагаемое); затраты страны, связанные с экономическим ущербом от привнесенного загрязнения (четвертое слагаемое).

 

1.                  Построение ТП-кооперативной игры

 

Рассмотрим кооперативную игру n лиц в форме характеристической функции. Игроками в этой игре являются страны-участницы процесса трансграничного взаимодействия. Обозначим множество всех игроков через . Используя функцию затрат (1) выпишем характеристическую функцию V(S) игры в следующем виде:

.                                                                      (2)

 

где  это вектор, компонентами которого являются объем выбросов стран-участниц коалиции S. Аналогично, .

Рассматриваемый способ построения характеристической функции показывает минимальное значение затрат, которое может гарантировать себе коалиция S, не координируя свои действия с другими игроками. При этом игроки, не входящие в коалицию S, стараются максимизировать затраты этой коалиции, т.е. действуют наихудшим для S образом [3], (см. также [2, 4]). Однако, на практике, подобное поведение очень часто вступает в конфликт с собственными интересами игроков (не входящих в коалицию S). Действительно, максимизируя затраты коалиции S можно достигнуть ситуации когда собственные затраты будут увеличиваться, что не всегда рационально для игроков. Для устранения этого противоречия, предположим, что каждый игрок j каким-либо образом (исходя из собственных интересов) определяет свою стратегию  в случае если он не вступает в коалицию с другим игроками, а действует самостоятельно.

Исходя из выше сказанного, характеристическую функцию игры можно выписать в виде [1]:

,                                                              (3)

 

или, в обозначениях сформулированной модели:

.

 

 

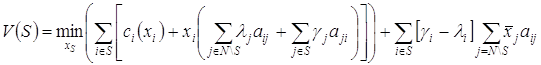Введем следующие обозначения:

, .

 

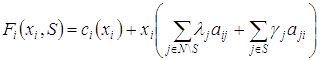Тогда, характеристическая функция игры вида (3) представима в виде:

,                                                   (4)

 

т.е. функция  зависит только от действий игроков , а функция  зависит только от действий игроков j, не входящих в коалицию S.

Пусть  — стратегия игрока , минимизирующая затраты коалиции S: . При этом, согласно ранее введенным обозначениям, мы можем найти значение из свойств производной:

.

 

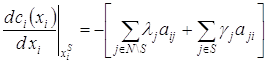Отметим, что единственность  зависит от вида функции , а числовое значение вычисляется в зависимости от конкретных игроков входящих в коалицию S (см. правую часть полученного выражения).

 

2.                   Условие супераддитивности

 

Для функций вида (3) и (4) условие супераддитивности было показано ранее [1]. Воспользуемся полученными результатами и выпишем введенное в [1] утверждение 1:

Утверждение 1. Для того чтобы характеристическая функция (4) удовлетворяла условию супераддитивности, достаточно, чтобы для любых  выполнялись условия: для всех ,  для всех  и  для всех .

При этом:  для ,  для  и  для  определяются следующим образом:

                         

 

 

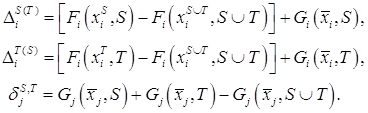
Рассмотрим более подробно условие . После небольших преобразований (в терминах поставленной задачи) получим выражение вида:

.

 

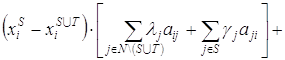
В случае не увеличения объема выбросов для игрока из коалиции S при объединении с коалицией T (т.е. ), второе слагаемое не отрицательное. Согласно введенным ограничениям для функции , при условии  будет выполняться  т.е. первое слагаемое тоже положительное. Однако, в силу условия , третье слагаемое не всегда является не отрицательным.

 

Литература

 

1.                  Акимова А.Н., Мельников В.В. – «Супераддитивность рациональной характеристической функции ТП-кооперативной игровой модели». Журнал научных публикаций аспирантов и докторантов. N1, с.101-103, 2015.

2.                  Васин А.А., Морозов В.В. – «Введение в теорию игр с приложениями в экономике». – М.: 2003.

3.                  Нейман Дж. фон, Моргенштерн О. – «Теория игр и экономическое поведение» (перев. с англ. под ред. и с доб. Н.Н.Воробьева). – М.: «Наука», 1970.

4.                  Петросян Л.А., Зенкевич Н.А., Семина Е.А. – «Теория игр». – М. 1998.

 

Поступила в редакцию 28.12.2015 г.