Применение матриц в практических задачах

 

Исламов Ёркин Абдухакимович,

старший преподаватель,

Садуллаева Мавжуда Зиёдуллаевна,

преподаватель.

Ташкентский автомобильно-дорожный институт, Республика Узбекистан.

 

Matrisalarni ba’zi amaliy masalalarga tadbiqlari

 

Y. A. Islomov,

TAYI, katta o’qituvchi ,

M. Z. Sadullayeva,

TAYI, o’qituvchi .

 

Matrisa matematikaning asosiy tushunchalaridan bo’lib, oliy tehnika o’quv ta’limgohlari dasturlari doiradasida o’rganiladi. Matrisalar chiziqli tenglamalar sistemalarini yechishda, shuningdek,mathematic dasturlash masalalarida keng qo’llaniladi. Quyida keltirilgan masalalarni matrisalar yordamida yechish ko’rsatilgan.

1. Quyidagi jadvalda tarmoqlarning reja davriga mo`ljallangan xarajat koeffisentlari va chekli mahsuloti shartli pul birligida berilgan.

 

Tarmoq		Iste`mol		Chekli mahsulot
		Sanoat	Qishloq xo`jaligi
Ishlab chiqarish	Sanoat	0,3	0,25	300
	Qishloq xo`jaligi	0,15	0,12	100

 

Quyidagilarni

a)                  Tarmoqlarning rejalashtirilgan yalpi mahsulot miqdorini, tarmoqlararo mahsulot yetkazib berish, tarmoqlarning sof mahsulotini;

b)                 Agar qishloq xo`jaligining chekli mahsuloti 20% ga, sanoatniki 10% ga oshirilsa, har bir tarmoqning zarur yalpi ishlab chiqarish miqdorini;

Topish kerak.

Yechish. a) To`g`ridan – to`g`ri xarajatlar koeffisentini A matrisa va chekli mahsulot vektori Y ni yozib olamiz:

 

bundan matrisani yozib olamiz.

 

U holda to`la xarajatlar matrisasi

 

(3.8) formula bo`yicha yalpi mahsulot vektori X ni aniqlaymiz:

 

Tarmoqlar mahsulot yetkazib berish miqdori x_ij ni formuladan topamiz. Masalan  

Tarmoqlarning yalpi mahsuloti, tarmoqlararo mahsulot yetkazib berish, shuningdek tarmoqlarning sof mahsulotlarini hisoblab topib, quyidagi jadvalni tuzamiz.

 

Tarmoq		Iste`mol		Chekli mahsulot	Yalpi mahsulot
		Sanoat	Qishloq xo`jaligi
Ichlab chiqarish	Sanoat	144,6	62,5	300	482
	Qishloq xo`jaligi	72,3	30	100	150
Sof mahsulot		265,1	157,5
Yalpi mahsulot		482	250

 

 b) Shartga ko`ra chekli mahsulot vektori

 

U holda (3.8) formulaga asosan mahsulot vektori quyidagicha bo`ladi:

 

Shunday qilib sanoatdagi ishlab chiqarishni 532,8 shartli pul birligigacha, qishloq xo`jaligida 287,1 shartli pul birligigacha oshirish kerak.

 

2. Oyoq kiyimlarni ishlab chiqaradigan fabrika S₁, S₂, S₃ xom ashyodan foydalanib 3 xil

mahsulot ishlab chiqaradi. Har bir juft oyoq kiyimiga xom ashyodan sarflanishi meyori quyidagi jadvalda berilgan.

 

Xom ashyo turi	Bir juft oyoq kiyimiga sarflanadigan xom ashyo miqdori			Bir kunda sarflanadigan xom ashyo
	Etik	Krasovka	Tufli
S1	4	2	3	1700
S2	1	3	1	1100
S3	7	1	4	2100

 

Bir kunda ishlab chiqariladigan har bir turdagi oyoq kiyimning sonini hisoblang.

Yechish. x₁, x₂, x₃ - mos ravishda etik, krasovka, tuflidan bir kunda ishlab chiqariladin oyoq kiyimlar soni. U holda har bir turdagi xom ashyoni sarflanishiga mos quyidagi sistemani tuzamiz:

 

 

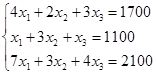
tuzilgan tenglamalar sistemasini Kramer usulidan foydalanib yechamiz:

 

 

 

 

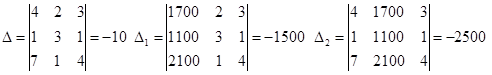
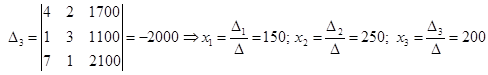
3. Korxona 3xil xom ashyodan foydalanib 3 xil mahsulot ishlab chiqaradi. Ishlab chiqarishning xarakteristikasi quyidagi jadvalda berilgan.

 

 

Berilgan xom ashyo zahirasidan foydalanib har bir tur mahsulotning ishlab chiqarish hajmini aniqlang.

Yechish. Mahsulot ishlab chiqarish hajmlarini x₁, x₂, x₃ lar bilan belgilaymiz. Zahirani to`la sarflash sharti bialn har bir tur xom ashyo uchun balans munosabatlarni quyidagi 3 ta no’malumli 3 ta tenglamalr sistemasi ko`rinishda yozib olamiz.

 

 

 

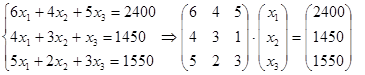
demak 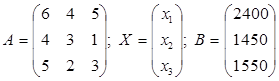 bo`lsa, A·X = B X = A^-1·B

 

 

 

 

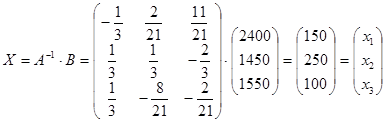
Adabiyotlar

 

1.                  Kремер Н. M. и другие. – «Высшая математика для экономистов» , - M.: 2004 г.

2.                  M. C. Kрасс, Б. П. Чупрынов. «Основы математики и ее приложения в экономическом образовании», - M.: Дело, 2000 г.

3.                  Соатов Ё.У. «Oлий математика», T.: Укитувчи, 1-жилд, 2-жилд, 1994 й., 3-жилд, 1996 й.

4.                  В. C. Шипачев «Курс высший математики», M.: Проспект, 2005 г.

 

Поступила в редакцию 14.03.2016 г.