Теоретическое обоснование возможности создания монотермического двигателя
Леонов Тарас Иванович,
радиоинженер.
The theoretical justification of the possibility of creating Mono-thermal motor
Taras Leonov,
radio engineer.
В статье предлагается рассмотрение поведения термодинамической системы, находящейся в гравитационном поле в неравновесном состоянии.
Ключевые слова: Ограниченность второго начала термодинамики.
This paper proposes consideration of the thermodynamic behavior of the system in a gravitational field in a non-equilibrium state.
Keywords: Limitation of the second law of thermodynamics.
В настоящее время в физике считается, что второе начало термодинамики является фундаментальным законом природы. Этот закон имеет множество формулировок и, к сожалению, очень часто используется как приговор при оценке работоспособности различных устройств, предлагаемых изобретателями, без тщательного анализа и исключением возможности их экспериментальной проверки. Однако, давайте в качестве контр примера рассмотрим работу следующего устройства (рис.1).
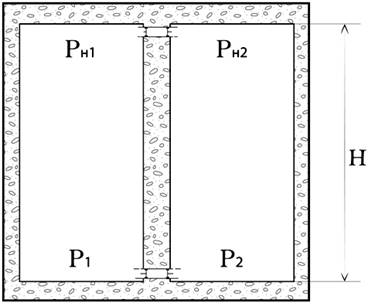
Рис. 1.
Имеем две теплоизолированные колонны (или шахты), наполненные одноатомным газом. Расположены они в гравитационном поле вертикально по отношению к поверхности планеты. Высота колонны = H, ускорение свободного падения = g. Параметры газа в основании первой колонны: давление – p1, температура – T1. В основании второй колонны: давление – p2, температура – T2. Между собой эти параметры связаны соотношением:
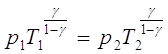 или
или 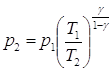 где
где ![]() - отношение теплоемкости газа при постоянном
давлении к теплоемкости при постоянном объеме. Как известно, для одноатомного
газа
- отношение теплоемкости газа при постоянном
давлении к теплоемкости при постоянном объеме. Как известно, для одноатомного
газа ![]() , а
, а ![]() и
и
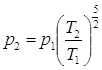 (1)
(1)
При таких
условиях мы можем адиабатно сжать некоторый объем газа V1 до объема
V2. в результате чего температура и давление этого газа станут
равными T2 и p2 соответственно, так как 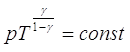 является формулой, справедливой именно
для адиабатного процесса.
является формулой, справедливой именно
для адиабатного процесса.
Количество работы, необходимого для сжатия газа определим по формуле:
 или
или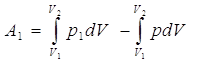 (2)
(2)
Первое слагаемое правой части уравнения – это та часть работы, которую произведет газ первой колонны, затратив при этом то же самое количество энергии. И, если общее количество газа, находящегося в первой колонне, намного больше объема V1 , то давление, оказываемое на сжимаемую порцию газа со стороны газа первой колонны можно считать постоянной величиной . Исходя из этого, первый интеграл будет равен p1*(V2-V1).
Если теперь,
исходя из хорошо известного равенства ![]() , где N
– количество молекул, содержащихся в объеме V, a k – постоянная Больцмана, и
также хорошо известного уравнения для адиабатного процесса
, где N
– количество молекул, содержащихся в объеме V, a k – постоянная Больцмана, и
также хорошо известного уравнения для адиабатного процесса![]() , получим:
, получим:
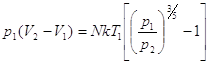
и, с учетом (1)
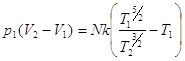 (3)
(3)
Второе слагаемое правой части уравнения (2) – это количество работы, которую нужно было бы произвести для адиабатного сжатия данного объема газа V1 до объема V2 , если бы это сжатие мы производили в вакууме. Для одноатомного газа
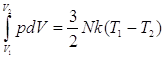 (4)
(4)
Итак, количество работы (2), необходимой для сжатия порции газа, состоящей из N молекул
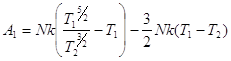 (5)
(5)
Теперь эту
порцию газа мы можем протолкнуть во вторую колонну. Причем, этот процесс будет
происходить при температуре T2 (по условию задачи) и при постоянном
давлении p2. (Общий объем второй колонны также намного больше объема
V2 Работа в этом процессе будет равна ![]() или,
используя известные равенства pV=NkT и
или,
используя известные равенства pV=NkT и
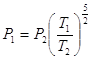 , получим:
, получим:
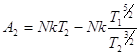 (6)
(6)
Суммарно, вся процедура сжатия и перемещения порции газа, состоящего и N молекул одноатомного газа из первой колонны во вторую потребует затрат внешних сил (количество работы) равных:
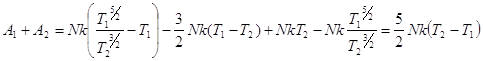 (7)
(7)
Отметим, что оба процесса являются обратимыми, так как процесс сжатия мы производим адиабатно, а процесс проталкивания этой порции газа производится при одной и той же температуре T2, как у сжатой порции газа, так и газа второй колонны.
Теперь попытаемся проделать то же самое в верхней части колонны.
Предположим, что температуры газов в обеих колоннах не зависят от высоты, а давления газов подчиняются закону распределения Больцмана. Тогда давление газа в верхней части первой колонны примет значение:
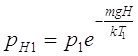
и во второй колонне:
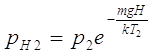
или, с учетом (1)
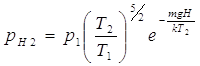
Объем порции газа, состоящей из того же количества N молекул:
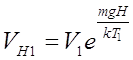
вверху первой колонны, и
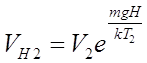
в верхней части второй колонны.
Если теперь адиабатно сжать выделенную порцию газа первой колонны с давлением газа PH1 и температурой T1 до некоторого давления P* и объема V* при которых ее температура станет равной T2, то работа внешних сил и работа AH1, которую выполнит остальной газ первой колонны будут те же самые, как и в первом случае, потому, что в конечном итоге она определяется по той же формуле (5). Однако, проделать работу по перемещению (проталкиванию) выделенной части газа из первой колонны во вторую без дополнительной работы не удастся, так как давление P* равное
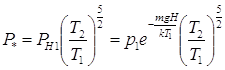 не равно PH2.
не равно PH2.
Поэтому, для того, чтобы начать проталкивать выделенную порцию газа, нужно довести ее давление до PH2. И, если мы хотим, чтобы этот процесс был также обратимым, то его нужно проводить при постоянной температуре, отводя от нее тепло за пределы системы.
Определим количество работы A* сторонних сил, необходимых для изотермического сжатия газа. Здесь также нужно учитывать, что часть работы выполнит газ первой колонны.
![]()
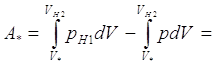
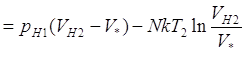 .
.
Здесь также первое слагаемое правой части уравнения выражает количество работы, производимой газом первой колонны, а второе – количество работы, которое нужно было бы затратить на сжатие выделенного объема газа, если бы мы его производили в вакууме. Теперь сжатую до давления pH2 порцию газа можно протолкнуть из первой колонны во вторую, затратив на этот процесс количество работы равное
![]()
Суммарно, вся процедура сжатия и перемещения порции газа, состоящего и N молекул одноатомного газа из верхней части первой колонны в верхнюю часть второй потребует затрат внешних сил (количество работы) равных:
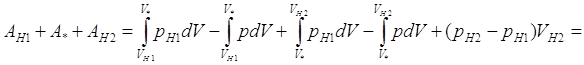
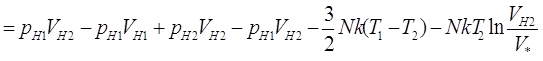
И, исходя из
предположения, что температуры газа от высоты не зависят (то есть равенство pV=NkT1
справедливо для любой части газа первой колонны и pV=NkT2
для второй) ![]() , а
, а ![]() и
и
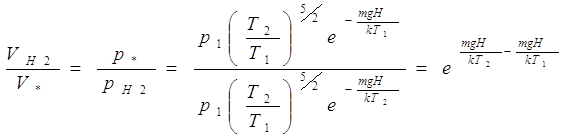 ,
,
получаем
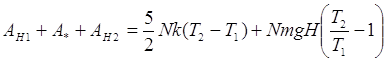 (8)
(8)
Здесь следует отметить, что все действия, которые мы производили в верхней части колонны, можно произвести и в обратном направлении. При этом работа будет производиться над внешними силами с поглощением тепла от внешнего источника при выполнении изотермического процесса (при выполнении работы A*) Таким образом, мы можем организовать термодинамический цикл, в который будет включен только один изотермический процесс расширения газа и в отличии от цикла Карно не используется изотермический процесс во время сжатия.
Если теперь просуммировать все работы в цикле с учетом знака, (положительные – когда работу производит сторонняя сила и отрицательные – когда работу производит система) получим:
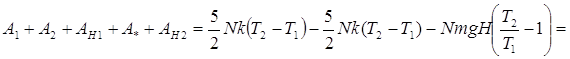
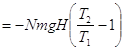 (9)
(9)
И, в соответствии с законом сохранения энергии, система должна получить извне такое же количество тепловой энергии:
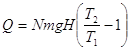 (10)
(10)
Кроме того следует отметить, что изотермический процесс можно проводить при любой другой температуре T, разумеется, переведя адиабатно выделенную порцию газа в соответствующее состояние. При этом работа изотермического процесса (и всего цикла) будет равна:
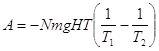 (11)
(11)
А количество тепловой энергии поглощаемой в цикле:
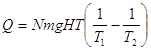 (12)
(12)
И величина, введенная и названая Клаузиусом приведенной теплотой, оказывается для рассматриваемого цикла постоянной величиной:
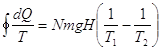 (13)
(13)
Рассматриваемая система, по сути, является системой, находящейся в неравновесном состоянии (газ в колоннах имеет разную температуру), а полученная формула (13) является характеристикой ее неравновесности. Наверно, следует еще раз подчеркнуть, что все рассуждения были проведены в предположении, что температура газов не зависит от высоты.
Из всего вышеизложенного можно сделать вывод, что предположение Больцмана о том, что газ, находящийся в гравитационном поле в состоянии термодинамического равновесия всюду имеет одинаковую температуру, вовсе не является препятствием для создания так называемого «вечного двигателя второго рода». Или – второе начало термодинамики не является фундаментальным законом природы.
Здесь возникает вопрос – где (и кем) была допущена ошибка. Для этого нам придется более подробно рассмотреть свойства идеального газа, находящегося в гравитационном поле. Но, об этом (и не только) – в следующей статье.
Литература
1. В.Г. Левич Курс теоретической физики Том 1, «Наука», Москва 1969.
2. Б.М.Яворский ,А.А.Детлаф Физика: для школьников старших классов и поступающих в вузы: Учеб. пособие. –М.:Дрофа, 1999 – 800с.:ил.
Поступила в редакцию 29.02.2016 г.