Автоматизированная система программного задания продольной подачи шлифовального круга
Еникеев Александр Фанилович,
доктор технических наук, доцент, Донбасская государственная машиностроительная академия,
Евсюкова Фатима Магометбиевна,
Национальный технический университет «ХПИ»,
Зыков Игорь Семенович,
кандидат технических наук, доцент, Национальный технический университет «ХПИ»,
Приходько Ольга Юрьевна,
кандидат технических наук, доцент, Национальный технический университет «ХПИ»,
Абрамская Инна Богдановна,
Украинский государственный университет железнодорожного транспорта.
Введение
Внедрение в машиностроительное производство современных информационных и энергосберегающих технологий базируется на разработке аппаратных средств автоматизации технологических процессов, в частности, алмазного шлифования (АШ). Программное задание автоматизированной компьютерной системой (АКС) поперечной и продольной подач алмазного инструмента, а так же его скорости вращения повышает производительность процесса АШ и обеспечивает заданное качество обработанной поверхности детали [5].
Целью статьи является разработка аппаратных средств АКС программного задания продольной подачи ШК, которые обладают нужной производительностью и точностью обработки входного сигнала. Достижение поставленной цели выполняется путем решения следующих задач:
· разработка критерия для оценивания производительности АКС;
· разработка математической модели АКС программного задания продольной подачи ШК;
· анализ производительности ее аппаратных средств.
Критерий оценивания производительности аппаратных средств
Управление продольной подачей АКС выполняет во время прямого или обратного хода ШК. Представим ее выходной сигнал в виде ограниченного ряда Фурье
![]() . (1)
. (1)
Оценим потери информации при дискретизации по времени аналогового сигнала (1). Динамическая погрешность дискретизации по времени аналогового сигнала исследована в работе [3]. Там же получено такое выражение для ее описания
![]() , (2)
, (2)
где m – количество интервалов дискретизации.
После преобразований выражения (2) имеем динамическую погрешность дискретизации гармонического сигнала в таком виде
![]() , (3)
, (3)
где Тпр – время выполнения ШК одного прохода.
После преобразований формулы (3) получим выражение для относительной погрешности дискретизации гармонического сигнала
![]() . (4)
. (4)
Среднеквадратическая погрешность дискретизации сигнала (1) оценивалась автором с учетом вкладов гармонических составляющих. Для получения ее оценки использовалось такое выражение
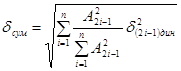 . (5)
. (5)
Результаты расчетов среднеквадратической погрешности дискретизации представлены на рис. 1. Задаваясь допустимым значением погрешности, получим с помощью графика минимально возможное количество интервалов дискретизации.
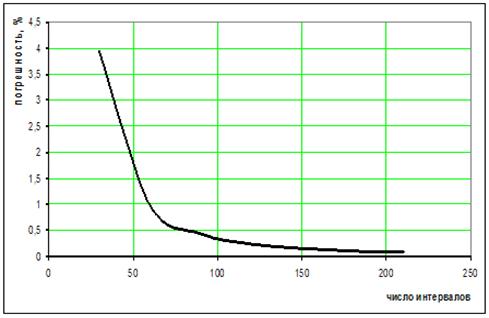
Рис. 1. График погрешности дискретизации выходного сигнала.
Разработка модели автоматизированной компьютерной системы
Выходной величиной АКС является угловая скорость вращения ШК. Передаточная функция исполнительного механизма (ИМ) описывается следующим выражением [2]
![]() , (6)
, (6)
где ![]() ,
, ![]() ,
, ![]() ,
,![]() ,
,![]()
![]()
![]()
![]()
![]() ,
, ![]() .
.
Анализ полюсов выражения (6) позволил без потери точности представить ИМ продольной подачи ШК такой передаточной функцией [1]
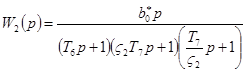 , (7)
, (7)
где ![]() – вычисляются по полученным корням.
– вычисляются по полученным корням.
Передаточная функция ИМ по возмущению получена в работе [1]
![]() . (8)
. (8)
В основу разработки АКС положен метод отработки рассогласования между измеренным значением продольной подачи ШК и ее оптимальным значением, которое хранится в банке данных процесса АШ. Структурная схема АКС представлена на рис. 2. Выполним разработку математических моделей компонент и анализ структурной схемы с целью получения выражения для передаточной функции.
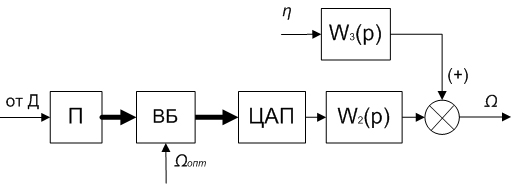
Рис. 2. Структурная схема АКС.
Специфика работы блоков Д и П в составе АКС позволяет представить их пропорциональным звеном с запаздыванием [3]
![]() , (9)
, (9)
где
![]() – коэффициент передачи и запаздывание.
– коэффициент передачи и запаздывание.
С
учетом полосы ![]() нечувствительности вокруг
номинальной характеристики имеем такую передаточную функцию блоков Д и П
нечувствительности вокруг
номинальной характеристики имеем такую передаточную функцию блоков Д и П
![]() . (10)
. (10)
Погрешность обработки входного сигнала блоками Д и П находит свое количественное выражение в нестабильности выходного кода. Для ее оценивания в работе [1] выполнена статистическая обработка экспериментальных данных
![]() .
.
Динамика ВБ и экстраполятора исследована в работе [4]. Передаточная функция АКС после преобразований получилась в таком виде
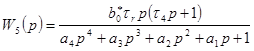 , (11)
, (11)
где ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Продольную подачу ШК представим в таком виде суммы экспоненциальных сигналов [4]
![]() ,
, ![]() . (12)
. (12)
Для вычисления интеграла Дюамеля применим обратное преобразование Лапласа к уравнению (7). После преобразований получим
![]() ,
, 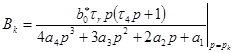 . (13)
. (13)
Интеграл свертки на основе выражений (12) и (13) дал уравнение, которое описывает выходной сигнал АКС. Это выражение описывает прогнозируемый выходной сигнал, который будет использован в дальнейшем при анализе производительности ее аппаратных средств
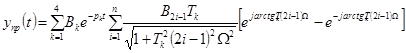 . (14)
. (14)
Для вычисления дискретной передаточной функции раскладываем выражение (7) на простые дроби
![]() , (15)
, (15)
где ![]() ,
, ![]() ,
, ![]() .
.
В соответствии с таблицей z-преобразований имеем такое выражение
![]() , (16)
, (16)
где ![]() ,
, ![]() ,
, ![]() .
.
Дискретная передаточная функция ИМ после преобразований получилась в виде отношения двух степенных полиномов
![]() , (17)
, (17)
где ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Блоки П и ВБ вносят запаздывание в работу АКС. Будем считать, что дискретное время запаздывания по входному сигналу составляет 2Т0. Следовательно, порядок модели d = 3. С учетом этого имеем такое выражение для передаточной функции
![]() . (18)
. (18)
Будем также считать, что возмущение приложено к механической части ИМ. Вычислим z-преобразования передаточной функции по возмущению
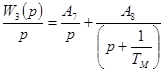 ,
, ![]() . (19)
. (19)
В соответствии с таблицей z-преобразований имеем такое выражение
![]() ,
, ![]() . (20)
. (20)
Дискретная передаточная функция ИМ по возмущению после преобразований получилась в виде отношения двух степенных полиномов
![]() . (21)
. (21)
После получения
выражений для дискретных передаточных функций перейдем к синтезу устройства
обработки сигнала продольной подачи ШК. Его синтез в
условиях действия помех выполним на основе минимизации квадратичного критерия
качества и с использованием эталонной математической модели. Процедура синтеза
приведена авторами к установлению параметров степенных полиномов ![]() ,
, ![]() ,
, ![]() и
и ![]() , при
которых основной контур устройства устойчив. Полином
, при
которых основной контур устройства устойчив. Полином ![]() определяет
динамику переходного процесса при устранении ошибки рассогласования основного
контура. Поскольку величиной погрешности
определяет
динамику переходного процесса при устранении ошибки рассогласования основного
контура. Поскольку величиной погрешности ![]() можно
задаться, а величина
можно
задаться, а величина ![]() интервала неопределенности уже
определена в результате статистической обработки экспериментальных данных, то
полином
интервала неопределенности уже
определена в результате статистической обработки экспериментальных данных, то
полином ![]() имеет вид
имеет вид
![]() . (22)
. (22)
Параметры
степенного полинома ![]() определяются так
определяются так
![]() , (23)
, (23)
где ![]() ,
, 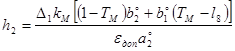 ,
, 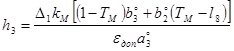 .
.
Входной сигнал
АКС представим функцией Хэвисайда с амплитудой ![]() .
Соответственно этот сигнал в форме z-преобразования имеет вид
.
Соответственно этот сигнал в форме z-преобразования имеет вид
![]() . (24)
. (24)
Для установившегося режима работы устройства обработки сигнала (ошибка рассогласования равняется нулю) имеем
![]() . (25)
. (25)
После
преобразований получим полином ![]() в таком виде
в таком виде
![]() ,
, ![]() ,
, ![]() ,
, ![]() . (26)
. (26)
При отсутствии входного сигнала имеем
![]() . (27)
. (27)
С учетом того,
что ![]() , имеем такое уравнение
, имеем такое уравнение
![]() .
.
Отсюда, после
преобразований получен полином ![]() в виде
в виде
![]() , (28)
, (28)
где ![]() ,
, 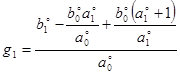 ,
, 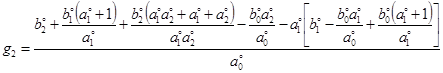 .
.
После преобразований получим передаточную функцию устройства обработки сигнала продольной подачи ШК в таком виде
![]() . (29)
. (29)
На основе выражений (14), (24) и (29) собрана схема компьютерного моделирования процессов преобразования информации АКС программного задания продольной подачи ШК (рис. 3).
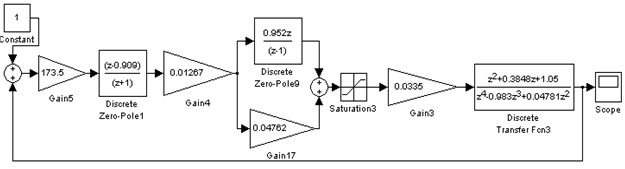
Рис. 3. Схема компьютерного моделирования.
Выводы
АКС реализует метод отработки рассогласований между измеренным значением продольной подач ШК и ее оптимальным значением, которое хранит банк данных процесса АШ. На основе дискретного преобразования Лапласа впервые построена математическая модель АКС. Статистической обработкой экспериментальных данных установлена зона нечувствительности датчика вокруг номинальной характеристики преобразования. На основе минимизации квадратичного критерия качества с использованием эталонной модели АКС синтезировано устройство обработки сигнала продольной подач ШК. Построена схема компьютерного моделирования процесса преобразования АКС входного сигнала. Время преобразования входного сигнала составило 0.06 с. Таким образом, производительность АКС программного задания продольной подачи ШК удовлетворяет требованиям по быстродействию.
Литература
1. Еникеев А.Ф. Анализ эффективности аппаратных средств управления продольной подачей шлифовального круга / А.Ф. Еникеев, Ф.М. Евсюкова, Л.А. Шишенко // Вестник Национального технического университета «ХПИ». – Харьков: №4, 2015. – С. 132 – 137.
2. Єнікєєв О.Ф. Комп’ютеризована система для підвищення ефективності алмазного шліфування / О.Ф. Єнікєєв, Т.Л. Щербак // Збірник наукових праць ІПМЕ НАН України. Випуск 63. – К.: 2012. – С. 32 – 40.
3. Еникеев А.Ф. Оптимальное управление технологическим процессом алмазного шлифования / А.Ф. Еникеев – Краматорск: ДГМА, 2001. – 160 с.
4. Еникеев А.Ф. Синтез цифрового регулятора поперечної передачі шліфувального круга / А.Ф. Еникеев, И.С. Зыков // Вестник Национального технического университета «ХПИ». – Харьков: №57, 2008. – С. 87 – 93.
5. Михелькевич В.И. Автоматическое управление шлифованием / В.И. Михелькевич – М.: Машиностроение, 1977. - 304 с.
Поступила в редакцию 11.04.2017 г.